Контрольная работа: Середні значення та їх оцінки
де n – число наведення дат або періодів;
Уn– останній член ряду;
У1–перший член ряду;
2. Метод відліку від умовного нуля
В практиці часто доводиться обчислювати середню арифметичну величину. Використовуючи властивості середньої арифметичної, можна значно спросити її обчислення:
- Середня сталої величини дорівнює цій самій сталій величині:
![]() (9)
(9)
- Сума відхилень від середньої, помножена на частоту, дорівнює нулю:
![]() (10)
(10)
- Якщо в усіх варіантах (Х) частота mоднакові; то середня арифметична зважена дорівнює середній арифметичній незваженій:
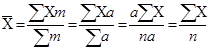 (11)
(11)
При m1 = m2 = ……= mn = a.
- Якщо від усіх варіантів (х) відняти сталу величину (хо) і за різницями (х – хо = х′ ) обчислити середню арифметичну (х′) , то вона буде менша від середньої арифметичної на таку саму величину хо′ з цього випливає, що середню з варіантів (х) можна дістати, додавши до знайденої середньої х′ ту саму постійну величину:
![]()
Якщо ![]()
- Якщо варіанти ( х) зменшити в однакове число разів, тобто поділити на постійну величину ( к), і з часток ![]() визначити середню, то вона буде зменшена в таке саме число разів, а тому, щоб дістати середню з варіантів (х) треба знайти середню (х′) і помножити її на ту саму величину (к): х = х′ ∙ к.
визначити середню, то вона буде зменшена в таке саме число разів, а тому, щоб дістати середню з варіантів (х) треба знайти середню (х′) і помножити її на ту саму величину (к): х = х′ ∙ к.
- Обчислюючи середню, замість абсолютних значень ваг (т) можна використати відносні величини ваг (відносні частоти):
![]() (12)
(12)
- Якщо в частотах (т) є спільний множник (А), то, обчислюючи середню, його можна не брати до уваги, тобто частоти можна скоротити на нього. При цьому середньої від заміни частот (т) на відповідні скорочені частоти (т)![]() не зміниться
не зміниться
![]()
- Загальна середня дорівнює зваженій середній з часткових середніх:
![]() (13)
(13)
Де хі – часткові середні (середні для окремих груп сукупності);
пі -- частоти окремих груп.
- Сума квадратів відхилень від середньої менша від суми квадратів відхилень від довільної величини (В) на величину поправки С, яка дорівнює добуткові об’єму сукупності на квадрат різниці між середньою і даною довільною величиною:
![]() (14)
(14)
Для випадку незваженої середньої і
![]() (15)
(15)
Для випадку зваженої середньої.
Література: