Контрольная работа: Системы массового обслуживания

Если выразить второй начальный момент через дисперсию, математическое ожидание и коэффициент вариации, то

,

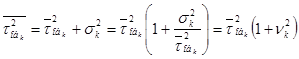где - коэффициент вариации, характеристика, показывающая степень нерегулярности потока заявок. Тогда среднее время ожидания

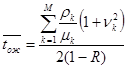(4)

Выражение (4) используем, чтобы найти среднее время ожидания заявки во второй фазе, для первой же фазы используем выражение (2). Затем по формуле (3) находим среднее время пребывания заявки в системе.

Производим сравнение полученных результатов при экспоненциальном распределении и неэкспоненциальном распределении.

4. Программа

//---------------------------------------------------------------------------

#pragma hdrstop

#include <iostream.h>

#include <string.h>

#include <conio.h>

//---------------------------------------------------------------------------

#pragma argsused

int main(int argc, char* argv[])

{

float a1,a2,ly=5,T1=0.15,T2=0.14,M1,M2,M,P00,P10,P01,P11;

a1=ly*T1;

a2=ly*T2;

P00=(1-a1)*(1-a2);//обе фазы свободны от заявок

P10=a1*(1-a1)*(1-a2);//в 1-й фазе заявка,2-я свободна

P01=a2*(1-a1)*(1-a2);//в 2-й фазе заявка,1-я свободна

P11=a1*a2*(1-a1)*(1-a2);//обефазызаняты

M1=a1/(1-a1);//среднее число заявок,находящихся в 1-й фазе

M2=a2/(1-a2);//среднее число заявок,находящихся в 2-й фазе

M=M1+M2;//Математическое ожидание числа заявок,находящихся в системе

cout<<'\n'<<"P00= "<<P00<<'\n'<<"P10= "<<P10<<'\n'<<"P01= "<<P01<<'\n'<<"P11= "<<P11<<'\n'<<"M1= "<<M1<<'\n'<<"M2= "<<M2<<'\n'<<"M= "<<M;

float toz1,toz2,tpreb1,tpreb2;//для экспон. и неэкспон. распределения соответственно

float R1,R2,k1=0.7,k2=0.8,k3=0.9;