Контрольная работа: Стабилизизация температуры воздуха в теплицах

Все коэффициенты характеристического уравнения положительны, что соответствует 1–му условию устойчивости для уравнения четвёртой степени.

Второе условие устойчивости.

Полученный результат показывает, что система устойчива.

Анализ устойчивости по критерию Найквиста.

Определим устойчивость САР температуры в теплице.

Передаточная функция разомкнутой системы.

Для определения устойчивости системы строим график, для чего рассчитываем значения модуля А(ω) и аргумента φ(ω) для разных значений ω.

ω	0	0.001	0.0015	0.002	0.0025	0.003	0.004	0.005	0.007
A(ω)	5	4.3	3.7	3.2	2.7	2.3	1.9	1.5	1
Φ(ω)	0	36	50	60	69	76	87	96	111
ω	0.009	0.01	0.015	0.02	0.03	0.04	0.045	0.05	0.07
А(ω)	0.78	0.68	0.4	0.23	0.1	0.05	0.039	0.03	0.012
Φ(ω)	123	127	149	166	190	206	212	217	237

Определение запасов устойчивости.

- что соответствует требуемым условиям.

7. Анализ зависимости статической ошибки системы от изменения управляющего воздействия на систему

в статике (при р = 0) получим:

где к – коэффициент передачи разомкнутой системы.

Таким образом:

Рассматриваемая система имеет статическую ошибку, пропорциональную изменению управляющего воздействия на систему.

8. Совместный анализ изменения управляемой величины объекта управления в статике. Определение статической ошибки системы по возмущающему воздействию

Передаточная функция САР по возмущающему воздействию.

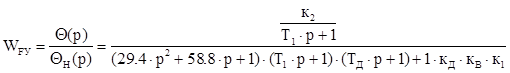
В статике при р = 0 получаем:

где