Контрольная работа: Статистичний аналіз діяльності комерційних банків (умовна вибірка показників по 20 банках)

Статистичні групування, за допомогою яких виявляють взаємозв’язки між ознаками, називають аналітичними[2].

Групування зводиться до утворення оптимального числа груп для кожного конкретного випадку з таким розрахунком, щоб групові середні носили не випадковий характер і щоб групувальна ознака проявила себе повною мірою.

Ранжируваний ряд – ряд, розташований в порядку збільшення або зменшення значень ознаки.

До характеристик центру розподілу відносять середню, моду та медіану.

Середня величина характеризує типовий рівень ознаки в сукупності.

Мода – це найпоширеніше значення ознаки, тобто варіанта, яка в ряду розподілу має найбільшу частоту. В інтервальному ряду за найбільшою частотою визначається модальний інтервал.

Моду обчислюють за наступною формулою:

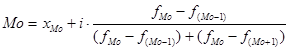(1.3)

де і –величина інтервалу; fMo – частота модального інтервалу; fMo-1 – частота інтервалу, що передує модальному; fMo+1 – частота інтервалу, наступного за модальним.

Моду визначають за гістограмою розподілу.

Медіана – це варіанта, яка припадає на середину упорядкованого ряду розподілу і ділить його на дві рівні за обсягом частини. В інтервальному ряду визначається медіанний інтервал.

Положення медіани визначається її номером.

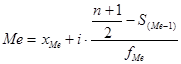(1.4)

де xMe – нижня границя медіанного інтервалу; і – величина інтервалу; S(Me-1) – накопичена частота інтервалу, що передує медіанному; f – частота медіанного інтервалу.

Середня величина в кожний момент часц чи на визначеному (котроткостро-ково-обмеженому) інтервалі часу характеризується наступними параметрами :

розмах варіації;

середнє лінійне відхилення;

середнє квадратичне відхилення;

дисперсію;

- коефіцієнт варіації.

Для вимірювання та оцінки варіації використовують абсолютні та відносні характеристики. До абсолютних відносяться: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсія; відносні характеристики представлені низкою коефіцієнтів варіації.

Варіаційний розмах характеризує діапазон варіації, це різниця між максимальним і мінімальним значеннями ознаки:

(1.5)

Узагальнюючою мірою варіації є середнє відхилення індивідуальних значень ознаки від центру розподілу.

Середнє лінійне відхилення:

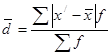(1.6)

Середнє квадратичне відхилення:

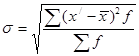(1.7)

Середній квадрат відхилень – дисперсія: