Контрольная работа: Свойства линейной прогрессии
После того, как была построена модель, необходимо проверить ее на адекватность.
Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: ![]() =0,827. Разброс данных объясняется линейной моделью на 82,7% и на 17,3% – случайными ошибками. Качество модели плохое.
=0,827. Разброс данных объясняется линейной моделью на 82,7% и на 17,3% – случайными ошибками. Качество модели плохое.
Проверим с помощью критерия Фишера.
Для проверки найдем величины: ![]() 345,19 и
345,19 и ![]() 6. Вычисляем k1 =1, k2 =13. Находим наблюдаемое значение критерия Фишера
6. Вычисляем k1 =1, k2 =13. Находим наблюдаемое значение критерия Фишера ![]() 57,6. Значимость этого значения a=0,00006, т.е. процент ошибки равен 0%, что меньше, чем 5%. Модель
57,6. Значимость этого значения a=0,00006, т.е. процент ошибки равен 0%, что меньше, чем 5%. Модель ![]() считается адекватной с гарантией более 95%.
считается адекватной с гарантией более 95%.
Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза ![]() , х=3000
, х=3000
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза: ![]()
Найдем полуширину доверительного интервала в каждой точке выборки xпр :

sе – средне квадратичное отклонение выборочных точек от линии регрессии ![]() 2,45
2,45
ty = критическая точка распределения Стьюдента для надежности g=0,9 и k2 =13.
n =15.
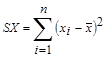
или ![]()
xпр – точка из области прогнозов.
Прогнозируемый доверительный интервал для любого х такой ![]() , где d(х=5000)=5,4, т.е. доверительный интервал для хпр =5000 составит от 14,08 до 25,01 с гарантией 90%.
, где d(х=5000)=5,4, т.е. доверительный интервал для хпр =5000 составит от 14,08 до 25,01 с гарантией 90%.
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область.
Т.е. при производительности труда 5000 грн уровень рентабельности составит от 14% до 25%.
Найдем эластичность.
Для линейной модели ![]()
![]()
Коэффициент эластичности показывает, что при изменении х=5000 на 1% показатель y увеличивается на 0,996%.
Обозначим фондоотдачу – Х, уровень рентабельности – У. Построим нелинейную зависимость показателя от фактора вида ![]() . Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений.
. Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений.
Минимальное значение Х=25.3, максимальное значение Х=49.3, значит, фондоотдача изменяется от 25.3 до 49.3грн. Минимальное значение У=10.9, максимальное значение У=28.3, уровень рентабельности изменяется от 10.9 до 28.3%. Среднее значение  . Среднее значение фондоотдачи составляет 38.4 грн, среднее значение уровня рентабельности составляет 18.93%.
. Среднее значение фондоотдачи составляет 38.4 грн, среднее значение уровня рентабельности составляет 18.93%.
Дисперсия ![]() =55.015,
=55.015, ![]() =33.16.
=33.16.
Среднеквадратическое отклонение ![]() 7.42, значит среднее отклонение фондоотдачи от среднего значения, составляет 7.42 грн.,
7.42, значит среднее отклонение фондоотдачи от среднего значения, составляет 7.42 грн., ![]() 5.76, значит среднее отклонение уровня рентабельности от среднего значения, составляет 5.76%.
5.76, значит среднее отклонение уровня рентабельности от среднего значения, составляет 5.76%.
Определим, связаны ли Х и У между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания) – нанесем точки ![]() на график.
на график.
Точка с координатами ![]() =(38.4; 18.93) называется центром рассеяния.
=(38.4; 18.93) называется центром рассеяния.
По виду корреляционного поля можно предположить, что зависимость между y и x нелинейная.
Пытаемся описать связь между х и у зависимостью![]() . Перейдем к линейной модели. Делаем линеаризующую подстановку:
. Перейдем к линейной модели. Делаем линеаризующую подстановку: ![]() ,
, ![]() . Получили новые данные U и V. Для этих данных строим линейную модель:
. Получили новые данные U и V. Для этих данных строим линейную модель: ![]()