Контрольная работа: Свойства линейной прогрессии
Параметры b0, b1 находим по МНК. 
Проверим значимость коэффициентов bi . Значимость коэффициента b может быть проверена с помощью критерия Стьюдента:
=-3,45. Значимость 
равна 0,004352681, т.е практически 0%. Коэффициент b0 статистически значим.
4,53. Значимость равна 0,00057, т.е практически 0%. Коэффициент b1 статистически значим.
Получили линейную модель 
После того, как была построена модель, необходимо проверить ее на адекватность.
Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: 
=0,62. Разброс данных объясняется линейной моделью на 62% и на 38% – случайными ошибками. Качество модели хорошее.
Проверим с помощью критерия Фишера.
Для проверки находим величины: 
284,224 и 
13,85. Вычисляем k1 =1, k2 =13. Находим наблюдаемое значение критерия Фишера 
20,53. Значимось этого значения a=0,00057, т.е. процент ошибки практически равен 0%. Модель считается адекватной с гарантией более 62%.
Так как линейная модель адекватна, то и соответствующая нелинейная модель тоже адекватна.
Находим параметры исходной нелинейной модели: а=b1 =-3,45; b = b0 =4,53.
Вид нелинейной функции: 
.
Т.е. зависимость уровня рентабельности от фондоотдачи имеет вид: .
Найдем прогноз на основании модели. Выберем произвольную точку из области прогноза [25.3; 49.3], х=1
Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза: 
Найдем полуширину доверительного интервала в каждой точке выборки. Для этого найдем полуширину для линейной модели:
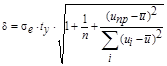
sе – средне квадратичное отклонение выборочных точек от линии регрессии 
3,721341
uпр – точка из области прогнозов. Прогнозируемый доверительный интервал для любого u такой 
Для нелинейной модели найдем доверительный интервал, воспользовавшись обратной заменой: 
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область.
Прогноз для х=1 составит от 5,31 до 22,58 с гарантией 90%.
Т.е. при фондоотдаче 1 грн. уровень рентабельности составит от 5.31% до 22.58%.
Найдем эластичность.
,
где 
Коэффициент эластичности для точки прогноза:
Коэффициент эластичности для точки прогноза: