Контрольная работа: Таблица производных Дифференцирование сложных функций
8. ![]() .
.
Зададим приращение аргументу ![]() , что даст
, что даст ![]() . Так как
. Так как ![]() , а
, а ![]() , то
, то ![]() . Отсюда
. Отсюда
 и
и 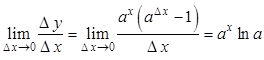 , то есть
, то есть ![]() .
.
Здесь была использована формула для одного из следствий из второго замечательного предела.
9. ![]() .
.
Для вычисления производной воспользуемся предыдущей формулой, в которой положим ![]() :
: ![]() . Значит,
. Значит, ![]() .
.
Прежде чем перейти к вычислению производных от обратных тригонометрических функций, рассмотрим вопрос о дифференцировании обратных функций вообще. Как было сказано в п. 8.2, для каждого взаимно однозначного отображения существует обратное отображение, то есть если ![]() , то
, то ![]() .
.
Теорема . Если для некоторой функции ![]() существует обратная ей
существует обратная ей ![]() , которая в точке
, которая в точке ![]() имеет производную не равную нулю, то в точке
имеет производную не равную нулю, то в точке ![]() функция
функция ![]() имеет производную
имеет производную ![]() равную
равную ![]() , то есть
, то есть 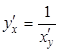 .
.
Доказательство. Рассмотрим отношение приращения функции к приращению аргумента: 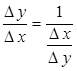 . Так как функция
. Так как функция ![]() имеет производную, то согласно теореме 11.2.2 она непрерывна, то есть
имеет производную, то согласно теореме 11.2.2 она непрерывна, то есть ![]() , откуда
, откуда 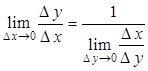 . Значит,
. Значит, 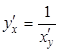 .
.
Воспользуемся данной теоремой для вычисления производных обратных тригонометрических функций.
10. ![]() .
.
В данном случае обратной функцией будет ![]() . Для нее
. Для нее ![]() . Отсюда
. Отсюда
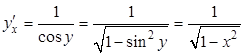 ,
,
то есть  .
.
11. ![]() .
.
Так как
![]() , то
, то 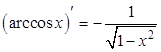 .
. ![]() .
.
В данном случае обратной функцией будет ![]() . Для нее
. Для нее
![]() .
.
Отсюда 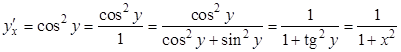 , то есть
, то есть ![]() .
.
13. ![]() .
.
Так как
![]() , то
, то ![]() .
.
2. Производная сложной функции
Пусть дана функция ![]() и при этом
и при этом ![]() . Тогда исходную функцию можно представить в виде
. Тогда исходную функцию можно представить в виде ![]() . Функции такого типа называются сложными. Например,
. Функции такого типа называются сложными. Например, ![]() .
.
В выражении ![]() аргумент
аргумент ![]() называется промежуточным аргументом. Установим правило дифференцирования сложных функций, так как они охватывают практически все виды существующих функций.
называется промежуточным аргументом. Установим правило дифференцирования сложных функций, так как они охватывают практически все виды существующих функций.
Теорема . Пусть функция ![]() имеет производную в точке
имеет производную в точке ![]() , а функция
, а функция ![]() имеет производную в соответствующей точке
имеет производную в соответствующей точке ![]() . Тогда сложная функция
. Тогда сложная функция ![]() в точке
в точке ![]() также будет иметь производную равную производной функции
также будет иметь производную равную производной функции ![]() по промежуточному аргументу умноженной на производную промежуточного аргумента по
по промежуточному аргументу умноженной на производную промежуточного аргумента по ![]() , то есть
, то есть ![]() .
.
Для доказательства дадим приращение аргументу ![]() , то есть от
, то есть от ![]() перейдем к
перейдем к ![]() . Это вызовет приращение промежуточного аргумента
. Это вызовет приращение промежуточного аргумента ![]() , который от
, который от ![]() перейдет к
перейдет к ![]() . Но это, в свою очередь, приведет к изменению
. Но это, в свою очередь, приведет к изменению ![]() , который от
, который от ![]() перейдет к
перейдет к ![]() . Так как согласно условию теоремы функции
. Так как согласно условию теоремы функции ![]() и
и ![]() имеют производные, то в соответствии с теоремой о связи дифференцируемости и непрерывности функции (теорема 11.2.2) они непрерывны. Значит, если
имеют производные, то в соответствии с теоремой о связи дифференцируемости и непрерывности функции (теорема 11.2.2) они непрерывны. Значит, если ![]() , то и
, то и ![]() , что, в свою очередь, вызовет стремление
, что, в свою очередь, вызовет стремление ![]() к нулю.
к нулю.
Составим ![]() . Отсюда,
. Отсюда,
