Контрольная работа: Вычисление пределов

Например, есть б. б. Ф при ; если б. б. ф. при действительно и

Теорема (о связи между функций, ее приделом и бесконечно малой функцией ). Если функция имеет придел, равный , то ее можно представить как сумму числа и бесконечно малой функции , т.е. если

Теорема (обратная). Если функцию можно представить в виде суммы числа А и б.м.ф. (x), то число А является пределом функции, т.е если , то

Например, требуется вычислить . Представим числитель и знаменатель в виде суммы числа и б.м.ф.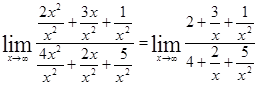

Функции при есть б.м.ф. таким образом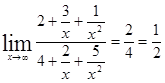

Основные теоремы о пределах

Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

Теорема справедлива для алгебраической суммы любого конечного числа функций.

Теорема 2. Функция может иметь только один предел при .

Теорема 3. Предел произведения двух функций равен произведению их пределов:

.

Следствие 1. Постоянный множитель можно выносить за знак предела:

Следствие 2. Предел степени с натуральным показателем равен той же степени предела: .

Теорема 4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю.

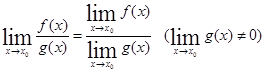
Примеры:

1)== ==

===

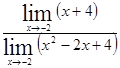2) =

=

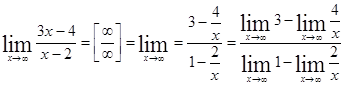3)

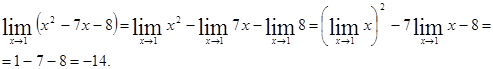
Первый замечательный предел

Второй замечательный предел

или

Примеры: