Контрольная работа: Вычисление случайных величин

Найдем дисперсию случайной величины Y:

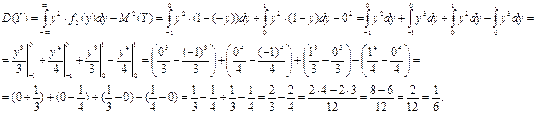
Найдем среднеквадратическое отклонение случайной величины Y:

Найдем математическое ожидание двумерной случайной величины (X,Y):

Тогда ковариация: ,

а значит и коэффициент корреляции

Следовательно, случайные величины X и Y - зависимые, но некоррелированные.

Задача №2

Двумерная случайная величина (X,Y) имеет следующее распределение вероятностей:

Y	X
	3	6	8	9
-0,2	0,035	0,029	0,048	0,049
0,1	0,083	0,107	0,093	0,106
0,3	0,095	0,118	0,129	0,108

Найти коэффициент корреляции между составляющими X и Y.

Решение.

Таблица распределения вероятностей одномерной случайной величины X:

X	3	6	8	9
	0,213	0,254	0,270	0,263

Проверка: + + + = 0,213 + 0,254 + 0,270 + 0,263 = 1.

Таблица распределения вероятностей одномерной случайной величины Y:

Y	-0,2	0,1	0,3
	0,161	0,389	0,450

Проверка: + + = 0,161 + 0,389 + 0,450 = 1.

Вычислим числовые характеристики случайных величин X и Y.

1. Математическое ожидание случайной величины X:

2.

Математическое ожидание случайной величины Y:

3. Дисперсия случайной величины X: