Контрольная работа: Высшая математика в экономике
1) определить потребности в сырье для выполнения плана по изготовлению стенок первого, второго, третьего и четвертого вида в количестве соответственно x1 , x2, x3 и x4 штук;
2) провести подсчеты для значений x1 = 50, x2 = 30, x3 = 120 и x4 =80.
Решение: составим условия для определения числа составных частей в зависимости от числа и вида комплектов мебели. Пусть n1 , n2 , n3 и n4 - число шкафов, шифоньеров, пеналов и тумб, соответственно.
Тогда условия будут выглядеть следующим образом:
n1 = x1 + x2
n2 = x1 + x2 + x4
n3 = x1 + x2 + x3
n4 = x1 + x2 + x3 + x4
Составим условия определяющие потребности в сырье в зависимости от вида деталей. Пусть y1 , y2 и y3 - потребности в стекле, ДВП и ДСП, соответственно:
y1 = 0,9n1 + 0,2n3 + 1,2n4
y2 = 6n1 + 6,5n2 + 6n3 + 2,5n4
y3 = 2,9n1 + 1,7n2 + 1,4n3 + 0,6n4
Теперь подставим вместо ni - полученные ранее равенства.
y1 = 0,9· (x1 + x2 ) + 0,2· (x1 + x2 + x3 ) + 1,2· (x1 + x2 + x3 + x4 )
y2 = 6· (x1 + x2 ) + 6,5· (x1 + x2 + x4 ) + 6· (x1 + x2 + x3 ) + 2,5· (x1 + x2 + x3 + x4 )
y3 = 2,9· (x1 + x2 ) + 1,7· (x1 + x2 + x4 ) + 1,4· (x1 + x2 + x3 ) + 0,6· (x1 + x2 + x3 + x4 )
Приведем подобные
y1 = 2,3x1 + 2,3x2 + 1,4x3 + 1,2x4, y2 = 21x1 + 21x2 + 8,5x3 + 9x4
y3 = 6,6x1 + 6,6x2 + 2x3 + 2,3x4
Проведем подсчеты для значений
x1 = 50, x2 = 30, x3 = 120 и x4 = 80
y1 = 2,3 * 50 + 2,3 * 30 + 1,4 * 120 + 1,2 * 80 = 448 кв. м.
y2 = 21 * 50 + 21 * 30 + 8,5 * 120 + 9 * 80 = 3420 кв. м.
y3 = 6,6 * 50 + 6,6 * 30 + 2 * 120 + 2,3 * 80 = 952 кв. м.
Задание 2
Пусть aij - количество продукции j, произведенной предприятием i, а bi - стоимость всей продукции предприятия i исследуемой отрасли. Значения aij и bi заданы матрицами A и В соответственно. Требуется определить цену единицы продукции каждого вида, производимой предприятиями отрасли. В ходе выполнения задания необходимо составить систему уравнений, соответствующую условиям, и решить ее тремя способами (матричный метод, метод Крамера, метод Гаусса).
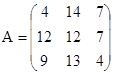 ,
, 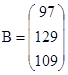
Решение:
Составим систему уравнений: