Контрольная работа: Взаимосвязь технико-экономических показателей работы предприятия и фондоотдачи



787,400

721,300

51667,580

47298,370

47357,410

;

.

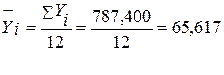
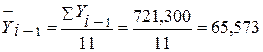
Проанализируем полученный результат. Если численное значение коэффициента автокорреляции находится в диапазоне от –0,3 до + 0,3, то принято считать, что существует автокорреляция между уровнями результирующего показателя. В нашем случае коэффициент автокорреляции составляет r = 0,691, следовательно, автокорреляция между уровнями фондоотдачи отсутствует. Это свидетельствует о том, что факторы, от которых зависит фондоотдача и которые даны нам в качестве исходной информации, являются основными, а влияние случайных, нам не известных факторов незначительно. По этой причине считаем, что искажение результатов моделирования будет несущественным, поскольку в модель будут включены только существенные факторы, от которых действительно зависит результирующая переменная.

5. Построение модели в стандартизированном виде

По характеру изменения уровней фондоотдачи можно выдвинуть гипотезу о прямолинейном законе распределения этого показателя во времени. Уравнение множественной регрессии для прямолинейной связи имеет следующий вид:

.

Для решения этого уравнения регрессии воспользуемся методом исключения (методом Гаусса), для чего составим и запишем систему нормальных уравнений:

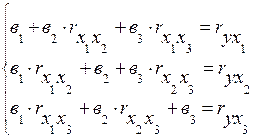
Решить систему нормальных уравнений – значит, найти численное значение коэффициентов регрессии , , . Все остальные параметры системы уравнений (коэффициенты парной корреляции) уже были вычислены на первом и втором этапах расчетов. Запишем эту же систему уравнений с численными значениями известных параметров:

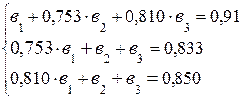
Разделим каждый член каждого уравнения системы на соответствующие коэффициенты при .

В результате этой процедуры (деления) получим новую систему уравнений с тремя неизвестными, в которой коэффициенты при , равны единице:

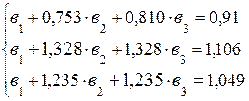
Для исключения из системы уравнений неизвестного параметра вычтем из второго уравнения – первое, и из третьего уравнения – первое. В результате этой операции (вычитания) получим новую систему из двух уравнений, но уже только с двумя неизвестными:

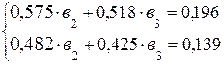
Как и в предыдущем случае, разделим каждый член каждого уравнения этой системы на соответствующие коэффициенты при .

В результате этой процедуры (деления) получим новую систему, состоящую из двух уравнений с двумя неизвестными, в которой коэффициенты при равны единице:

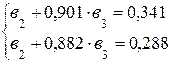
Для исключения из этой системы уравнений неизвестного параметра вычтем из второго уравнения первое. В результате этой операции (вычитания) получим новое уравнение, но уже только с одним неизвестным:

.

Откуда

Для определения численного значения коэффициента регрессии подставим найденное значение коэффициента регрессии в первое уравнение системы из двух уравнений: