Курсовая работа: Алгоритмы поиска кратчайших покрытий булевых матриц

ВВЕДЕНИЕ

Микроэлектроника является одним из наиболее быстро и эффективно развивающихся направлений науки и техники. Однако вместе с развитием схемотехники увеличивается и сложность разрабатываемых схем. Существуют элементы схемы, логической моделью которых является матрица, в частности, булева. Площадь микросхемы и ее быстродействие во многом зависят от параметров матрицы. Поэтому приоритетной задачей является уменьшение размеров элемента, например, путем нахождения кратчайшего покрытия булевых матриц. Целесообразность поиска кратчайших покрытий возникает и при минимизации ДНФ булевых функций, при синтезе логических схем некоторых типов, при решении систем логических уравнений, при поиске простейших диагностических тестов, а так же во многих других задачах, эффективность методов решения которых, оказывается, существенно зависящей от совершенства используемых алгоритмов поиска кратчайших покрытий.

Алгоритмы нахождения кратчайших покрытий – занятие трудоемкое для человека, особенно при сравнительно большой размерности матрицы, поэтому разработанная мною программа значительно упрощает выполнение этой работы.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим задачу о переводчиках [1]. Допустим, из некоторого числа переводчиков, каждый из которых владеет несколькими определенными языками, требуется скомплектовать минимальную по числу членов группу такую, чтобы она смогла обеспечить перевод с любого из интересующих нас языков.

Решение данной задачи легко находиться с помощью нахождения кратчайшего покрытия булевой матрицы, составленной по условию.

Если обозначить множество переводчиков, из которого можно производить выбор, через A={a, б, в, г, д}, а множество интересующих нас языков через B={1,2,3,4,5,6}. То можно ввести булеву матрицу C отношения переводчиков к языкам.

1 2 3 4 5 6

.

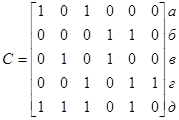Это означает, что переводчик а знает языки 1,3, переводчик б – языки 4,5 и т.д.

Таким образом, данная задача сводится к задаче нахождения кратчайшего покрытия булевой матрицы С, то есть нахождения такой минимальной совокупности строк матрицы, которая содержала бы не менее одной единицы в каждом столбце матрицы.

2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Булевой матрицей называется матрица, элементы которой – либо 0, либо 1.

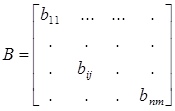, {0, 1}.

Говорят, что i-я строка покрывает j-й столбец, если на их пересечении стоит единица, то есть =1. Причем каждая строка обязательно покрывает некоторое подмножество столбцов, а каждый столбец покрывается хотя бы одной строкой.

Подмножество строк матрицы B, в совокупности покрывающее все ее столбцы, образует строчное покрытие этой матрицы.

Подмножество столбцов матрицы B, в совокупности покрывающее все ее строки, образует столбцовое покрытие этой матрицы.

Покрытие, содержащее минимальное число строк (столбцов) матрицы B, называется кратчайшим покрытием матрицы B.

Пример1.

1 2 3 4 5 6 7 8 9 10

.

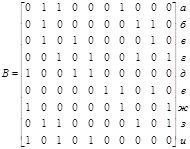Множество строк матрицы B {а, в, г, е, ж} – одно из строчных покрытий этой матрицы. Множество же строк {д, е, з} – одно из кратчайших строчных покрытий матрицы B.

3. АЛГОРИТМЫ ПОИСКА КРАТЧАЙШИХ ПОКРЫТИЙ

Ниже приведены алгоритмы нахождения кратчайших покрытий методом Патрика [5] и методом Закревского [1].

3.1 Метод Патрика

Если требуется найти все кратчайшие покрытия булевой матрицы, можно найти все ее покрытия и выделить из них кратчайшие. Это реализуется на следующем примере.

Пример 2. Для матрицы

.

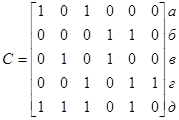распишем, какие строчки покрывают определенный столбец в виде дизъюнкций.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--