Курсовая работа: Алгоритмы поиска кратчайших покрытий булевых матриц
(а Ú д)(в Ú д)(а Ú г Ú д)(б Ú в)(б Ú г Ú д)г = авг Ú бгд Ú вгд Ú абвг Ú бвгд Ú абвгд.
Отсюда видно, что кратчайшее покрытие булевой матрицы С – либо {а, в, г}, либо {б, г, д}, либо {в, г, д}.
Это нахождение покрытий перебором на ЭВМ реализуется для исходной матрицы небольшого размера (до 7 х 7), чтобы реализовать метод Патрика для немногим больших матриц, рекомендуется оптимизировать матрицу.
3.2 Метод Закревского
Аркадий Дмитриевич Закревский предложил довольно эффективный и простой способ нахождения малой величины покрытия булевой матрицы (так называемое разложение по минимальному столбцу и минимальной строке).
Замечание: все случаи просчитывались как вручную, так и на ЭВМ при помощи разработанной программы.
3.2.1 Строчное покрытие
Алгоритм нахождения строчного покрытия методом Закревского:
1. Ищется столбец с минимальным числом единиц. Если таковых несколько, то выбирается любой (для определенности, допустим, самый левый).
2. Среди строк, покрывающих этот столбец, ищется строка с максимальным числом единиц и заносится в покрытие (следовательно, удаляется из матрицы); если же таких строк несколько, то выбирается любая из них (для определенности, допустим, самая верхняя).
3. Удаляются все столбцы, которые покрывает полученная строка.
Действия продолжаем до тех пор, пока не удалится вся матрица.
Пример 3. Найдем кратчайшее строчное покрытие матрицы С:
1 2 3 4 5 6
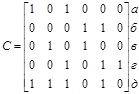 .
.
1. Столбец 6 содержит минимальное число единиц – 1.
2. Строка г заносится в покрытие и удаляется из матрицы.
3. Удаляются столбцы 3, 5, 6.
Получаем матрицу
1 2 4
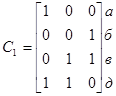 .
.
Далее проводим аналогичные действия с матрицей С:
1. Столбец 1 (самый левый) содержит только 2 единицы.
2. Строка д, покрывающая этот столбец, покрывает 2 столбца, заносится в покрытие и удаляется из матрицы.
3. Удаляются столбцы 1, 2.
Остался только один столбец матрицы – 4. Можно выбрать как строку б, так и строку в, в обоих случаях мы имеем покрытие матрицы, состоящее из 3 строчек.
Итого получаем покрытия {б, г, д} и {в, г, д } – как показал метод Патрика – кратчайшие покрытия.
Замечание: Не всегда метод Закревского дает кратчайшее покрытие, оно может состоять и из большего числа строк, но находится быстрее.
Столбцовое покрытие