Курсовая работа: Алгоритмы поиска подстроки в строке
Сравнения текста и образца могут производиться в любом порядке.
|
Турбо - БМ является также является улучшением алгоритма Боуера - Мура. Мы будем запоминать сегмент текста, который сошелся с суффиксом образца во время прошлой попытки (и только, если произошел сдвиг хорошего суффикса).
Это даст нам два преимущества:
1. Возможность перескочить через этот сегмент
2. Возможность применения «турбо – сдвига»
«Турбо – сдвиг» может произойти, если мы обнаружим, что суффикс образца, который сходится с текстом, короче, чем тот, который был запомнен ранее.
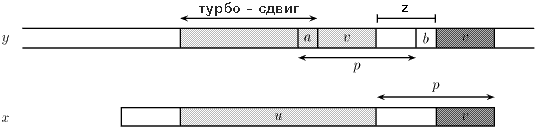
Пусть u - запомненный сегмент, а v - cуффикс, совпавший во время текущей попытки, такой что uzv - суффикс x. Тогда av - суффикс x, два символа а и b встречаются на расстоянии p в тексте, и суффикс x длины |uzv| имеет период длины p, а значит не может перекрыть оба появления символов а и b в тексте. Наименьший возможный сдвиг имеет длину |u| - |v| ( его мы и называем «турбо – сдвигом» ).
1.5. Поиск подстрок с помощью конечного автомата.
1.5.1. Структура автомата.
По определению, конечный автомат представляет собой пятерку М = (Q, q0 , A, 
, 
), где:
Q — конечное множество состояний;
q0 
Q — начальное состояние;
А
Q — конечное множество допускающих состояний;
— конечный входной алфавит;
— функция Q х 
Q, называемая функцией переходов автомата.
Первоначально конечный автомат находится в состоянии q0 . Затем он по очереди читает символы из входной строки. Находясь в состоянии q и читая символ а, автомат переходит в состояние (q,a). Если автомат находится в состоянии q 
A говорят, что он допускает прочитанную часть входной строки. Если q 
А, то прочитанная часть строки отвергнута.
С конечным состоянием М связана функция 
, называемая функцией конечного состояния, определяемая следующим образом: 
есть состояние, в которое придет автомат (из начального состояния), прочитав строку w. Автомат допускает строку w тогда и только тогда, когда А
Для каждого образца Р можно построить конечный автомат, ищущий этот образец в тексте. Первым шагом в построении автомата, соответствующего строке-образцу Р[1..m], является построение по Р вспомогательной суффикс-функциии (как в алгоритме КМП). Теперь определим конечный автомат, соответствующий образцу Р[1..m], следующим образом:
· Его множество состояний Q = {0,1,..., m}. Начальное состояние q0 = 0. Единственное допускающее состояние m;
· Функция переходов определена соотношением (q — состояние, 
— символ): (q,a) = 
(Pq a). (1)
Поясним это соотношение. Требуется сконструировать автомат таким образом, чтобы при его действии на строку Т соотношение
(Тi ) = (Тi )
являлось инвариантом (тогда равенство (Тi ) = m будет равносильно тому, что Р входит в Т со сдвигом i — m, и автомат тем самым найдет все допустимые сдвиги). Однако в этом случае вычисление перехода по формуле (1) необходимо для поддержания истинности инварианта, что следует из теорем, приведенных ниже.[3]
Теорема. Пусть q = (х), где х — строка. Тогда для любого символа а имеет место (ха) = (Pq a).
Теорема. Пусть — функция конечного состояния автомата для поиска подстроки Р[1.. m]. Если Т[1.. n] — произвольный текст, то (Тi ) = (Тi ) для i=0,1,..., n. [14]
Из изложенного следует, что задача поиска подстроки состоит из двух частей:
построение автомата по образцу (определение функции переходов для заданного образца);
применение этого автомата для поиска вхождений образца в заданный текст.
1.5.2. Пример построения конечного автомата
Построим конечный автомат, допускающий строку ababaca. Поскольку длина образца m = 7 символов, то в автомате будет m + 1 = 8 состояний.
Найдем функцию переходов . В соответствии с определением (1), (q, a) =(Рq а), где — префикс-функция, а — произвольный символ из алфавита , q — номер состояния. Таким образом, необходимо для каждого префикса Pq = P[0..q], q = 0 .. m образца Р и для всех символов а входного алфавита найти длину максимального префикса Р, который будет являться суффиксом строки Рq а. Длина этого префикса и будет значением функции переходов (q,a). Если а = P[q + 1] (очередной символ текста совпал со следующим символом образца), то Рq а = Рq +1 и (q, a) = q+1.