Курсовая работа: Алгоритмы сжатия данных

Дня данной таблицы символов коды Хаффмана будут выглядеть следующим образом.

А 0

Б 100

В 101

Г 110

Д 111

Поскольку ни один из полученных кодов не является префиксом другого, они могут быть однозначно декодированы при чтений их из потока. Кроме того, наиболее частый символ сообщения А закодирован наименьшим количеством битов, а наиболее редкий символ Д - наибольшим.

Классический алгоритм Хаффмана имеет один существенный недостаток. Дня восстановления содер­жимого сжатого сообщения декодер должен знать таблицу частот, которой пользовался кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию сообщения. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по сообщению: одного для построения модели сообщения (таблицы частот и Н-дерева), другого для собственно кодирования.

Арифметическое кодирование

Алгоритм арифметического кодирования

Арифметическое сжатие - достаточно изящный метод, в основе которого лежит очень простая идея. Мы представляем кодируемый текст в виде дроби, при этом строим дробь таким образом, чтобы наш текст был представлен как можно компактнее. Для примера рассмотрим построение такой дроби на интервале [0, 1) (0 - включается, 1 - нет). Интервал [0, 1) выбран потому, что он удобен для объяснений. Мы разбиваем его на подынтервалы с длинами, равными вероятностям появления символов в потоке. В дальнейшем будем называть их диапазонами соответствующих символов.

Пусть мы сжимаем текст "КОВ.КОРОВА" (что, очевидно, означает "коварная корова"). Распишем вероятности появления каждого символа в тексте (в порядке убывания) и соответствующие этим символам диапазоны:

Символ	Частота	Вероятность	Диапазон
О	3	0.3	[0.0; 0.3)
К	2	0.2	[0.3; 0.5)
В	2	0.2	[0.5; 0.7)
Р	1	0.1	[0.7; 0.8)
А	1	0.1	[0.8; 0.9)
“.”	1	0.1	[0.9; 1.0)

Будем считать, что эта таблица известна в компрессоре и декомпрессоре. Кодирование заключается в уменьшении рабочего интервала. Для первого символа в качестве рабочего интервала берется [0, 1). Мы разбиваем его на диапазоны в соответствии с заданными частотами символов (см. таблицу диапазонов). В качестве следующего рабочего интервала берется диапазон, соответствующий текущему кодируемому символу. Его длина пропорциональна вероятности появления этого символа в потоке. Далее считываем следующий символ. В качестве исходного берем рабочий интервал, полученный на предыдущем шаге, и опять разбиваем его в соответствии с таблицей диапазонов. Длина рабочего интервала уменьшается пропорционально вероятности текущего символа, а точка начала сдвигается вправо пропорционально началу диапазона для этого символа. Новый построенный диапазон берется в качестве рабочего и т. д.

Используя исходную таблицу диапазонов, кодируем текст "КОВ.КОРОВА":

Исходный рабочий интервал [0,1).

Символ "К" [0.3; 0.5) получаем [0.3000; 0.5000).

Символ "О" [0.0; 0.3) получаем [0.3000; 0.3600).

Символ "В" [0.5; 0.7) получаем [0.3300; 0.3420).

Символ "." [0.9; 1.0) получаем [0,3408; 0.3420).

Графический процесс кодирования первых трех символов можно представить так, как на рис. 4.

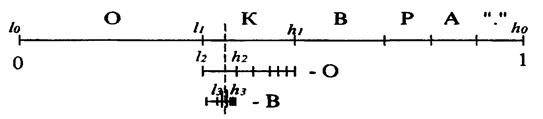
Рис. 4. Графический процесс кодирования первых трех символов

Таким образом, окончательная длина интервала равна произведению вероятностей всех встретившихся символов, а его начало зависит от порядка следования символов в потоке. Можно обозначить диапазон символа с как [а[с]; b[с]), а интервал для i-го кодируемого символа потока как [l_i , h_i ).

Большой вертикальной чертой на рисунке выше обозначено произвольное число, лежащее в полученном при работе интервале [/_i , h_i ). Для последовательности "КОВ.", состоящей из четырех символов, за такое число можно взять 0.341. Этого числа достаточно для восстановления исходной цепочки, если известна исходная таблица диапазонов и длина цепочки.

Рассмотрим работу алгоритма восстановления цепочки. Каждый следующий интервал вложен в предыдущий. Это означает, что если есть число 0.341, то первым символом в цепочке может быть только "К", поскольку только его диапазон включает это число. В качестве интервала берется диапазон "К" - [0.3; 0.5) и в нем находится диапазон [а[с]; b[с]), включающий 0.341. Перебором всех возможных символов по приведенной выше таблице находим, что только интервал [0.3; 0.36), соответствующий диапазону для "О", включает число 0.341. Этот интервал выбирается в качестве следующего рабочего и т. д.

Реализация алгоритма арифметического кодирования

Ниже показан фрагмент псевдокода процедур кодирования и декодирования. Символы в нем нумеруются как 1,2,3... Частотный интервал для i-го символа задается от cum_freq[i] до cum_freq[i-1]. Пpи убывании i cum_freq[i] возрастает так, что cum_freq[0] = 1. (Причина такого "обpатного" соглашения состоит в том, что cum_freq[0] будет потом содеpжать ноpмализующий множитель, котоpый удобно хpанить в начале массива). Текущий pабочий интеpвал задается в [low; high] и будет в самом начале pавен [0; 1) и для кодиpовщика, и для pаскодиpовщика.

Алгоритм кодирования:

С каждым символом текста обpащаться к пpоцедуpе encode_symbol(). Пpовеpить, что "завеpшающий" символ закодиpован последним. Вывести полученное значение интеpвала [low; high).