Курсовая работа: Анализ избирательных цепей в частотной и временной областях
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ;(1.3)
;(1.3)
![]() .
.
Временная диаграмма входного сигнала изображена на рис. 1.1.
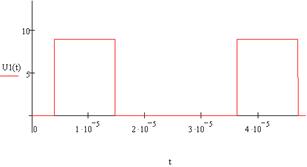
Рисунок 1.1 – Временная диаграмма входного сигнала
2. Определение дифференциального уравнения относительно отклика цепи по методу уравнений Кирхгофа
Составим систему уравнений согласно первым и вторым законами Кирхгофа для мгновенных значений токов и напряжений (2.1):
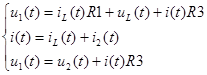 .(2.1)
.(2.1)
Из первого уравнения (2.2):
![]() .(2.2)
.(2.2)
Из второго уравнения (2.3):
![]() .(2.3)
.(2.3)
Из третьего уравнения (2.4):
![]() .(2.4)
.(2.4)
Подстановка (2.4) в уравнение (2.3) дает (2.5):
![]() .(2.5)
.(2.5)
Подстановка (2.5) в уравнение (2.2) дает (2.6):
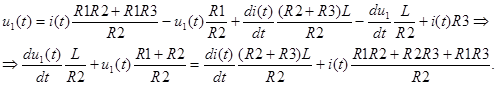 (2.6)
(2.6)
3. Расчет временных характеристик цепи
Переходная характеристика цепи имеет вид (3.1):
![]() ,(3.1)
,(3.1)
гдеA – постоянная интегрирования;
![]() – принужденная составляющая (3.2). Находится в установившемся режиме (при
– принужденная составляющая (3.2). Находится в установившемся режиме (при ![]() ) при условии воздействия на входе постоянного напряжения 1 вольт:
) при условии воздействия на входе постоянного напряжения 1 вольт:
![]() ;(3.2)
;(3.2)
![]() .
.
Чтобы определить постоянную интегрирования А, найдем начальное значение ![]() (3.3). Индуктивности в момент времени
(3.3). Индуктивности в момент времени ![]() эквивалентна разрыву.
эквивалентна разрыву.
![]() ;(3.3)
;(3.3)