Курсовая работа: Анализ избирательных цепей в частотной и временной областях

Тогда (3.4):

;(3.4)

.

После подстановки числовых значений переходная характеристика имеет вид:

.

Импульсную характеристику найдем, используя связь между переходной и импульсной характеристиками (3.5):

.(3.5)

По полученным выражениям рассчитаем временные характеристики (табл. 3.1) и построим графики (рис. 3.1 и рис.3.2).

Таблица 3.1 – Расчет временных характеристик

,	0	1.2	2.4	3.6	4.8	6	7.2	8.4	9.6	10.8
,	0.029	0.037	0.04	0.041	0.042	0.042	0.042	0.042	0.042	0.042
,	10.204	4.184	1.716	0.704	0.289	0.118	0.049	0.02	0.008	0.003

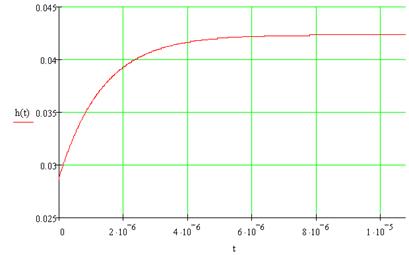
Рисунок 3.1 – График переходной характеристики

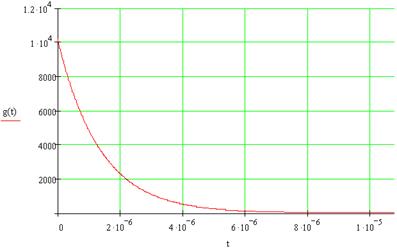
Рисунок 3.2 – График импульсной характеристики

4. Расчет отклика цепи временным методом

Расчет отклика произведем при помощи переходной характеристики.

Отклик определяется на входной сигнал. Поскольку за время, которое равно времени периоду Т входного сигнала, временные характеристики практически примут значения принужденной составляющей, отклик на периодический входной сигнал можно найти как повторный отклик на входной сигнал в виде отдельного прямоугольного импульса:

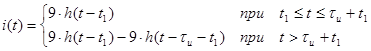.(4.1)

Таблица 4.1 – Расчет отклика цепи временным методом

,	0	2	4	6	8	10	12	14	16	18	20
, мА	0	0	0	351.98	374.25	379.29	380.44	380.69	50.97	11.54	2.61

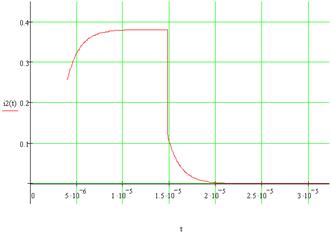
Рисунок 4.1 – Временная диаграмма отклика

5. Расчет частотных характеристик цепи

Комплексный коэффициент передачи:

;

.

Тогда:

.(5.1)

После подстановки числовых значений имеем (5.2):

, См.(5.2)

АЧХ – модуль ; ФЧХ – аргумент , т.е.:

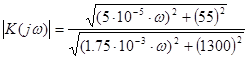, См;(5.3)

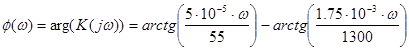, рад. (5.4)