Курсовая работа: Анализ современных цифровых радиоприемных устройств

При t=kΔ, имеем . Обозначив решение уравнения (58) можно искать в виде:

Подставляя (8) в (7) получаем характеристическое уравнение, определяющее λ:

При найденных корнях уравнения (9) или (6) λk=zk, k=1,M, общее решение уравнения (7) можно представить в виде:

где ограниченные коэффициенты А1, А2, …Аm определяются начальными условиями.

Для момента времен с номером (k+1) из (10) следует:

Если все полюса системной функции (5) удовлетворяют условию

т.е. они лежат внутри единичного круг с центром в точке z=0, то на основании (10) и (11) можно прийти к заключению, что все свободные колебания во времени определяются членами бесконечно убывающей геометрической прогрессии и фильтр будет устойчивым.

Недостатком рассмотренной схемы рекурсивного ЦФ является наличие отдельных элементов задержки для входных и выходных отсчетов.

Это недостаток устранен в так называемой канонической схеме рекурсивного ЦФ, использующего общие элементы задержки для входных и выходных отсчетов, при M=L.

a₀

a₁

a₂

Z-1

Z-1

Z-1

x(k) a_L

b₁

b₂

b_M

Каноническая схема реализации рекурсивного ЦФ

Рисунок 8.

Каноническая схема идентична ранее рассмотренной схеме рекурсивного ЦФ.

Чтобы это доказать, определим системную функцию ЦФ по канонической схеме. Обозначим значения дискретного отсчета в k-й момент времени на выходе первого сумматора через W(k). Согласно схеме, очевидна справедливость уравнения

Дискретный сигнал на выходе второго сумматора в k-й момент времени

Выполним Z-преобразование над правой и левой частями (13-14). Получим:

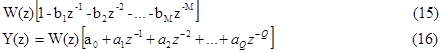
Приравняв значения W(z) из (15) и (16), имеем