Курсовая работа: Анализ тепломассообмена
Определение температурного напора при переменных температурах. Уравнение (5) для теплового потока записано при условии постоянства температур Тf 1 и Тf 2 . Это допущение справедливо, если количество переносимой теплоты намного меньше теплосодержания охлаждаемой и нагреваемой сред. Если это условие не выполняется, то отвод теплоты от более нагретой среды будет уменьшать ее температуру, а подвод теплоты к более холодной среде будет ее температуру увеличивать. Найдем температурный напор в уравнении (5) при переменных значениях температур Tf 1 и Тf 2 . Обозначим TfI = Тг , Тf 2 =Тх .
Уравнение теплового потока. Поток теплоты через единицу поверхности теплообмена dА: dQ = Kp ·(Tг – Tx )dA = Kp ·∆TdA (7), где Кр – коэффициент теплоотдачи через единицу поверхности теплообмена; Тг , Тх – текущие переменные температуры греющей и нагреваемой сред (в дальнейшем индекс "г" будем относить к греющей среде, индекс "х" - к холодной).
Тепловой поток dQ при водит к увеличению температуры холодной среды и уменьшению температуры нагретой среды
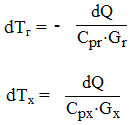
d(Tг – Tx ) = d(∆T) = - dQ·[1/(Cp г ·Gг )+1/( Cpx ·Gx )]
где Срг , Срх - теплоемкость горячей и холодной среды при P=const; Gг ,Gx - массовый расход горячей и холодной среды, кг/с.
Обозначим 1/(Cp г ·Gг )+1/( Cpx ·Gx ) = n. Тогда dQ = - d(∆T)/n (8).
Интегрируя последнее уравнение в пределах от начального значения ∆Т=∆Т' до конечного значения ∆Т=∆Т" при n=const, получим уравнение потока теплоты Q = (∆Т' - ∆Т")/n (9), где ∆Т' = Тг ' – Тх ', ∆Т" = Тг " – Тх "; Тг ', Тг " – начальная, конечная температуры нагретой среды; Тх ', Тх " – начальная, конечная температуры холодной среды. Тогда
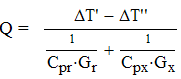
Среднелогарифмический перепад температур. Подставляя значения dQ из (8) в (7), получим: - d(∆Т)/n = Kp ·∆ТdA.
Интегрируя это уравнение в пределах от начального значения ∆Т=∆Т' до конечного значения ∆Т=∆Т" по всей поверхности теплообмена А, получим: ln(∆Т'/∆Т") = Kp ·n·A. Подставляя значение n из уравнения (9) в последнее уравнение, найдем
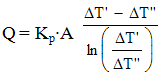
Обозначим ∆Тср = (∆Т' - ∆Т'')/ln(∆Т'/∆Т'') - среднелогарифмический температурный напор.
Введем среднеарифметический температурный напор ∆Тср а : ∆Тср а = (∆Т' + ∆Т'')/2.
Отношение среднеарифметического перепада ∆Тср а к среднелогарифмическому ∆Тср равно
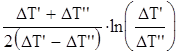
∆Тср а /∆Тср =
При ∆Т'/∆Т''→1, ∆Тср →∆Тср а во всех других случаях ∆Тср < ∆Тср а . Средний перепад при переменных температурах нагретой и холодной сред используют при расчете переноса теплоты в теплообменных аппаратах.
ЗАДАНИЕ
Исследовать эффективность оребрения поверхности плоской стенки в зависимости от высоты ребра h, коэффициент теплопроводность материала λ при граничных условиях третьего рода.
Плоская стенка оребрена по высоте продольными ребрами прямоугольного сечения высотой h и толщиной 2δ. Стенка имеет размеры по высоты 800 мм и ширине 1000 мм. По ширине стенки размещено 50 ребер. Для оптимального размера ребра произвести расчеты распределения температуры по высоте ребра, определить плотность потока теплоты по высоте ребра, определить плотность потока теплоты, передаваемой ребром. Оценить вклад отвода теплоты к воздуху оребренной поверхностью стенки по сравнению с неоребренной.
Исходные данные:
Длина ребра: l = 800 мм
Высота ребра: h = 10;20;30мм
Толщина ребра: b = 1,0 мм
Материал ребра: латунь
Температура воздуха: tв = 20°С
Температура поверхности у основания ребра: tс = 100°С
Скорость движения воздуха: ω = 10;5 м/с