Курсовая работа: Анализ тепломассообмена

Выполнила: ст. гр. ТЭН-312

Ибрагимов Т.Г.

Принял: проф. Минаев Б.Н.

Москва 2008

Передача теплоты через оребренную поверхность плоской стенки.

Оребрение поверхности позволяет уменьшить внешнее термическое сопротивление l/α·A за счет увеличения поверхности теплообмена А. С этой целью обычно используют оребрение внешних поверхностей. Кроме того, оребрение может непосредственно воздействовать на интенсивность теплообмена в пограничном слое и коэффициент конвективной теплоотдачи α. Рассмотрим влияние оребрения внешней поверхности на теплообмен. Схема оребрения показана на рис.1.

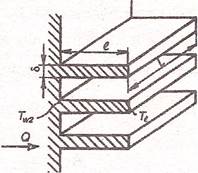
Рис.1. Поверхность нагрева с ребрами прямоугольного сечения: δ - толщина ребра; l - высота ребра; L – длина ребра; T_{w 2} – температура у основания ребра; T_l – температура на вершине ребра

Площадь оребренной поверхности А_2,р = A_р + A_м , где A_р - площадь ребер, A_м - площадь межреберного пространства, T_{w 2} - температура межреберной· поверхности, α₂ - коэффициент теплоотдачи от оребренной поверхности.

Тепловой поток с межреберной поверхности Q_м = α₂ ·А_м ·(Т_{w 2} –T_{f 2} ).

Тепловой поток с поверхности ребер Q_р =α₂ ·А_р ·(Т_{w 2} – T_{f 2} )·ψ_р .

Общий тепловой поток с оребренной поверхности Q_2,р =α₂ ·(А_м +ψ_р ·А_р )·(Т_w2 –T_f2 ), где ψ_р =Q/Q_max (1). Допускаем, что коэффициент теплоотдачи α₂ одинаков для межреберной поверхности и поверхности ребер (что верно до определенного предельного расстояния между двумя соседними ребрами).

Допускаем, что коэффициент теплоотдачи α₂ одинаков для межреберной поверхности и поверхности ребер (что верно до определенного предельного расстояния между двумя соседними ребрами).

Перенос теплоты через оребренную поверхность. Paссмотрим процесс переноса теплоты через оребренную с внешней стороны стенку при граничных условиях III рода. Тепловой поток Q можно записать следующим образом:

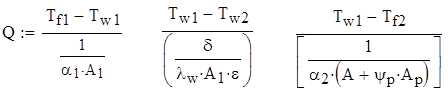
где индексы "1" и "2" относятся, соответственно, к внутренней и внешней поверхностям; ε_ф - коэффициент, учитывающий влияние формы стенки; для плоской стенки ε_ф =l.

Введем полное термическое сопротивление R_р ^* , м² ·К/Bт, оребренной поверхности

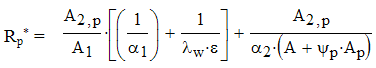
и коэффициент теплопередачи через оребренную поверхность К_р , Вт/(м² ·К)

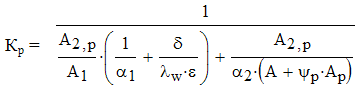
отнесенные к единице площади оребренной поверхности А_2,р .

Тогда

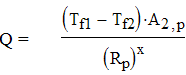
Q = К_р ·А_2,р ·(Т_{f 1} -T_{f 2} ).

Так как величина ψ_р всегда меньше единицы, то суммарный эффект оребрения будет определяться совокупным воздействием увеличения отношения площадей теплообмена A_2,р /А₁ и достигаемой величиной ψ_р . По мере увеличения высоты ребра с ростом площади оребрения одновременно уменьшается средняя температура ребра и, соответственно, величина ψ_р . Поэтому существуют оптимальные размеры оребрения (высота и толщина ребер, их число, расстояние между ними), при которых передаваемая теплота становится максимальной и делает оребрение наиболее эффективным.

Эффективность оребренuя. Так как оребрение снижает термическое сопротивление только оребренной поверхности, то оно будет эффективно лишь в том случае, если другие составляющие общего термического сопротивления (материала, неоребренной поверхности)

существенно меньше. Это означает, что чем больше l/α₂ по сравнению с 1/α₁ и δ/λ_w ·ε_ф , тем выше эффективность оребрения.

Критерий эффективности оребрения может быть приближенно найден следующим образом. Очевидно, что оребрение целесообразно лишь в том случае, если тепловой поток с боковой поверхности ребра А_р = П·lбольше, чем тепловой поток с основания ребра А_f .

Следовательно величина ψ_р ^' должна быть значительно больше единицы. Выражение для ψ_р ^' можно записать в виде:

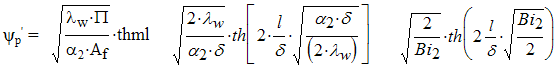
--> ЧИТАТЬ ПОЛНОСТЬЮ <--