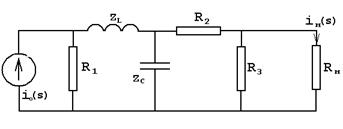
Курсовая работа: Анализ цепи во временной области различными методами Анализ цепи

Приведем выражение в скобках к синусу по Эйлеру (умножим и разделим на ):

Амплитудный спектр входного сигнала:

Фазовый спектр входного сигнала:

Ширина спектра определяется по графику:

с^-1 ;

3.1. Сопоставляя соответственно спектры входного сигнала с частотными характеристиками цепи, дадим заключение об ожидаемых искажениях сигнала на выходе цепи.

Можно установить, что приблизительно одна десятая часть амплитудного спектра входного сигнала укладывается в полосу пропускания, а фазочастотная характеристика в этой полосе имеет гиперболическую зависимость, в отличие от прямолинейной фазочастотной характеристики входного сигнала. Таким образом, при прохождении через цепь входной сигнал будет в значительной степени искажен. На выходе цепи можно ожидать сигнал, значительно более слабый, чем поданный на вход, и более выраженный по своей продолжительности. Этот качественный вывод подтверждается точным расчетом в п.2 (см. Рис.4)

4. Анализ цепи частотным методом при периодическом воздействии

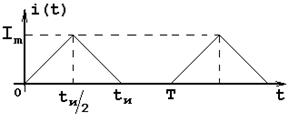
Разложим в ряд Фурье заданный входной периодический сигнал. Построим его амплитудный и фазовый спектры.

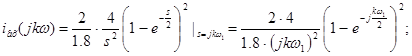
Для получения амплитудного и фазового дискретного спектра выделим модуль и фазу, для этого выражение сведем к синусу по Эйлеру (умножим и разделим на ):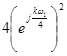

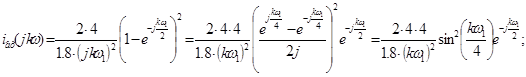
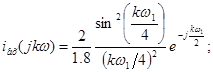
Амплитудный дискретный спектр: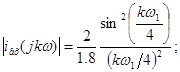

Фазовый дискретный спектр:

	0	1	2	3	4	5	6
	1.111	0,856	0,354	0,041	0,011	0,052	0,03
	0	-1.745	-3.491	-5.236	-3,84	-8.727	-10.472

Построение входного периодического сигнала и его аппроксимации отрезком ряда Фурье

Число гармоник ряда Фурье определяется шириной спектра по уровню : 2 гармоники (см. Рис.10)

Построение амплитудного и фазового спектров выходного периодического сигнала, используя рассчитанные в п.3.1 АЧХ и ФЧХ функции передачи цепи. Запись тока на выходе цепи в виде отрезка ряда Фурье