Курсовая работа: Анализ условий формирования и расчет основных статистических характеристик стока реки Кегеты

1969

1970

1971

1972

1973

1974

1975

2.67

2.30

2.88

3.56

2.30

2.72

2.64

1.96

2.26

Вследствие недостаточной длины рядов наблюдений за годовым стоком (как правило не превышают 60…80 лет, составляя в основном 20…40 лет) норма годового стока, определенная по (17) отличается от истинного среднего значения Q_N на величину σ_Qn тогда:

Q_N =Q_{0 n} ±σ_{Qn ,} (18)

где Q_{0 n} – средний годовой сток за ограниченный период наблюдений; σ_Qn – средняя квадратическая ошибка n-летней средней.

Cогласно теории ошибок, величина σ_Qn , на которую отличается среднее значение годового стока за n лет от истинной нормы Q_N за N лет при N®∞, равна

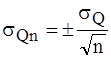(19)

где σ_Q – среднее квадратическое отклонение единичных значений годового стока Q_i от среднего за n лет.

Определяется σ_Q по формуле

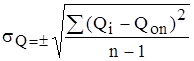. (20)

Для сравнения точности определения нормы стока рек различной водности пользуются относительным значением средней квадратической ошибки. Так, выражая σ_Q в процентах от Q_0n получим среднюю, квадратическую ошибку нормы стока, вычисленную по ограниченному ряду n лет,

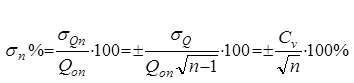, (21)

где – коэффициент вариации ряда годовых значений стока за n лет.

Коэффициент вариации C_V характеризует колебания годовых значений стока относительно их средней величины. Он является безразмерной характеристикой изменчивости годового стока, удобной для сравнения нескольких рядов наблюдений, различающихся своими средними значениями. При выражении отдельных членов ряда в безразмерных модульных коэффициентах K_i коэффициент вариации определяется по формуле

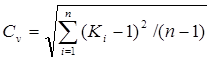. (22)