Курсовая работа: АРТ-моделирование на фондовом рынке

Коэффициент корреляции обладает следующими свойствами:

1). Коэффициент не имеет размерности, следовательно, сопоставим для различных статистических показателей;

2). Величина коэффициента корреляции лежит в пределах от -1 до +1. Значение |ρ_{x , y} | = 1 свидетельствует о том, что между переменными существует функциональная зависимость, т. е. все наблюдения лежат на одной прямой (чем ближе |ρ_{x , y} | к 1, тем ближе эта связь к функциональной); если ρ_{x , y} равен или приближается к нулю, это указывает на отсутствие линейной связи между X и Y, хотя допустимо существование нелинейной зависимости;

3). Если значение ρ_{x , y} > 0 (коэффициент корреляции положителен), то взаимосвязь величин прямая: с ростом Х увеличивается Y. Отрицательный коэффициент корреляции говорит об обратной взаимосвязи.

Наличие связи между X и Y может быть обнаружено, если: а) Х есть причина Y; б) Y есть причина Х; в) если Х и Y совместно зависимые величины; г) если Х и Y являются следствием некоторой общей для них причины.

В практике статистического анализа имеют место случаи, когда корреляционный анализ обнаруживает существование достаточно сильной зависимости признаков, в действительности не имеющих причинно-следственной связи между собой, – такие корреляции называют ложными.

Оценка коэффициента корреляции, определенная по выборке, является случайной величиной, поэтому необходимо проверить гипотезу о значимости, т. е. проверить предположение, существенно ли коэффициент корреляции отличается от нуля, или это случайное отклонение, связанное с выборкой. Если ρ_{x , y} - коэффициент корреляции в генеральной совокупности, то нулевая гипотеза может быть как:

,

и альтернативная ей

.

В качестве критерия применяют статистику, которая для выборки (х, y) из нормальной генеральной совокупности будет иметь t-распределение. Ее вычисляют по формуле:

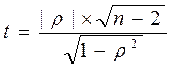. (3)

Расчетное значение критерия сопоставляют с табличным значением распределения Стьюдента t _{α , ν} , где ν - число степеней свободы, ν = n - 2, α - уровень значимости. Если получают t > t _{α , ν} , то нулевая гипотеза отвергается и можно утверждать, что коэффициент корреляции значим. В случае t < t _{α , ν} нет оснований отвергать нулевую гипотезу и следует сделать заключение о том, что коэффициент корреляции незначим[11] .

Прикладные цели регрессионного анализа в области экономики заключаются в следующем:

1). Установить наличие статистически значимой регрессионной связи между зависимой и объясняющими переменными;

2). Определить конкретный аналитический вид связи;

3). Спрогнозировать и восстановить значения исследуемого результирующего показателя по известным значениям объясняющих переменных.

Таким образом, построение эконометрической модели является основой любого эконометрического исследования. Она выступает в качестве средства анализа и прогнозирования в различных сферах: финансовой, производственной, инвестиционной, и применяется для исследования объектов самого разного уровня – от отдельных предприятий, отраслей, регионов до страны в целом.

Регрессионная модель представляет собой один из основных типов эконометрических моделей. Она отражает зависимость случайного результирующего показателя y от одной или нескольких детерминированных объясняющих переменных Х = (x₁ , x₂ , …, x_p ).

Выявление регрессионной зависимости осуществляется на основе анализа данных о наблюдениях за экономическими процессами, которые образуют выборки из генеральной совокупности. При построении эконометрических моделей желательно, чтобы все выборочные распределения используемых показателей соответствовали нормальному закону распределения.

Математическую модель регрессионной зависимости можно записать следующим образом:

, (4)

где f ( X ) представляет собой детерминированную составляющую модели, в которой Х выступает как вектор объясняющих переменных Х=(х ₁ , х _{2, ... ,} х _p ) ;

ε – остаточная компонента (возмущение модели).

Детерминированная составляющая модели f ( X ) выражает влияние существенных факторов на зависимый показатель y и описывает условное математическое ожидание:

. (5)

Случайная составляющая отражает суммарное влияние всех несущественных факторов.

В данном случае нас интересует множественная линейная регрессия стоимости ценных бумаг от различных экономических факторов.

Множественной регрессией называют модель, которая включает несколько предсказывающих или объясняющих переменных. Она полнее объясняет поведение зависимой переменной и позволяет сопоставить влияние включенных в уравнение регрессии факторов.