Курсовая работа: АРТ-моделирование на фондовом рынке
В общем виде модель множественной линейной регрессии, включающая p объясняющих переменных х 1 , ..., х p имеет вид:
![]() , (6)
, (6)
где β 0 , β 1 , ..., β p – неизвестные оцениваемые параметры регрессии;
х 1, х 2 , …, х p - влияющие факторы; ε – остаточная компонента.
Задача оценивания в данном случае заключается в том, чтобы с помощью метода наименьших квадратов найти такие оценки b 0 , b 1 , …,b p , которые минимизировали бы квадраты отклонений наблюдаемых значений зависимой переменной yi от расчетных значений, вычисленных с помощью уравнения регрессии.
Функция, значение которой минимизируют с помощью МНК:
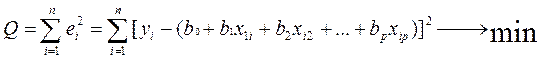 . (7)
. (7)
Оценки параметров регрессии, получаемые по методу наименьших квадратов, обладают статистическими свойствами несмещенности, состоятельности и эффективности.
Свойство несмещенности оценок заключается в том, что оценки параметров b j , найденные с помощью линейного МНК, не содержат систематических ошибок при оценивании. Свойство состоятельности означает, что при росте объема выборки до бесконечности с вероятностью, близк?