Курсовая работа: Автокорреляционные функции и энергетические спектры погрешностей наблюдений
Для равенства (3.70)
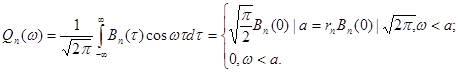 (3.74)
(3.74)
Для равенства (3.73)
 (3.75)
(3.75)
Можно также пользоваться выражениями (3.71) и (3.72), но только для получения отдельных прикидочных оценок или с целью получения менее громоздких выражений из интегралов.
Для трехмерных аномалий, предполагая значения ошибок наблюдений симметричными относительно вертикальной оси, автокорреляционные функции ошибок наблюдений для законов, аналогичных равенствам (3.70) и (3.73) двухмерного случая, опишем соответственно формулами
Bп (τ)н = 2J1 (eτ) / eτ, (3.76)
Bп (τ)н = exp(-pτ)J0 (tτ) (3.77)
при следующих наиболее вероятных значениях постоянных [38]:
e = 2,4 / Δx, p = 0,5 / Δx, t = 1,5 / Δx.
Для энергетических спектров ошибок наблюдений, определяемых равенствами (3.76), (3.77), получим соответственно следующие выражения [для равенства (3.77) из-за громоздкости выражения приводим значение Qп (0)]:
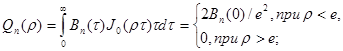 (3 78)
(3 78)
![]() (3.79)
(3.79)
Связь между энергетическими характеристиками исходных и трансформированных аномалий
Выразим энергетический (взаимный энергетический) спектр или корреляционную функцию трансформированной аномалии через энергетический (взаимный энергетичекий) спектр или корреляционную функцию исходной аномалии.
Так как спектр трансформированной аномалии ST выражается через спектр S [см. равенство (2.5)], то на основании формулы (3.16) для энергетического спектра трансформированной аномалии получим
QT (u,v) = Q(u,v)|Ф(u,v)|2 , (3.80)
где Q — спектр исходной аномалии, а Ф - частотная характеристика преобразования. Из этой формулы можно получить энергетический спектр трансформированной аномалии, зная энергетический спектр исходной и частотную характеристику преобразования. Пользуясь равенствами (2.5), (3.17), такое же соотношение можно написать и для взаимных энергетических спектров:
QT (u,v)12 = Q(u,v)12|Ф(u,v)|2 . (3.81)
Что же касается корреляционных функций (автокорреляционной и взаимной корреляционной), то, как видно из равенств (3.12), (3.15), (3.20), (3.80), (3.81), для получения корреляционной функции трансформированной аномалии по известной корреляционной функции исходной необходимо последнюю подвергать трансформации с частотной характеристикой |Ф(u,v)|2 . Все это верно и для двухмерного случая. Рассмотрим несколько частных случаев.
1. Аналитическое продолжение на уровень Н аномалий в области верхнего или нижнего полупространства
Как известно, в этом случае
Ф(u,v) = ехр(±ρH),
где знак "минус" относится к аналитическому продолжению в области верхнего полупространства, знак "плюс" - в области нижнего. Тогда
|Ф(u,v)|2 = ехр(±2ρH).
Отсюда видно, что для получения корреляционной функции, аналитически продолженной на уровень Н в области верхнего или нижнего полупространства аномалии, необходимо корреляционную функцию исходной аналитически продолжить на уровень 2Н. На основании этого положения для корреляционных функций можно записать интеграл Пуассона, заменив в нем значение Н на значение 2Н.
2. Вычисление n-й горизонтальной производной
В этом случае (рассматриваем произвольную по оси x)
Ф(u,v) = (iu)n . (3.82)
Следовательно,
|Ф(u,v)|2 = u2 n = (-1)n (iu)2 n . (3.83)
Аналогичный результат получим и при дифференцировании по направлению оси у. Из последних двух равенств видно, что для получения корреляционной функции аномалии n-й горизонтальной производной необходимо продифференцировать корреляционную функцию исходной аномалии по направлению соответствующей оси 2n раз и умножить полученный результат на (-1)n . Например, для оси x верно равенство
![]() (3.84)
(3.84)
где B(ξ, η) и Bn (ξ, η) - автокорреляционные функции исходной аномалии и аномалии n-й производной по направлению оси х.
3. Вычисление n-й вертикальной производной
Так как для данного случая
Ф(ρ) = (-ρ)n , (3.85)
то
|Ф(ρ)|2 = (-ρ)2 n . (3.86)
Отсюда видно, что вывод такой же, как и в предыдущем случае, только результат не нужно умножать на (-1)n . На основании этого положения в двухмерном и трехмерном случаях для автокорреляционных функций получим
![]() (3.87)
(3.87)
где B(τ) и Bn (τ) - автокорреляционные функции исходной аномалии и аномалии n-й вертикальной производной (здесь учтено, что в выражение B(τ) глубина залегания аномального тела входит в виде 2h).