Курсовая работа: Автоматическая система регулирования промышленного кондиционера

0 0 0.0001 0

0 0 0.0000 0

0 0 0 0.0001

0 0 0 0.0000

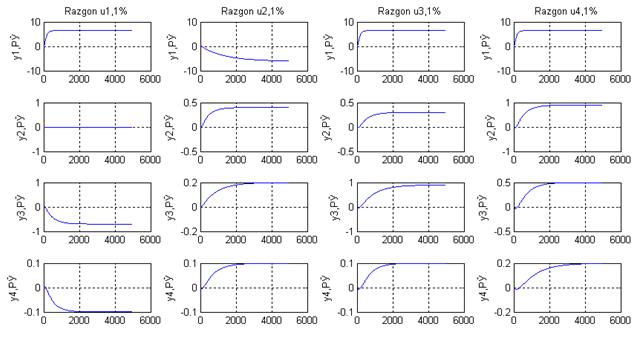Рисунок. Кривые разгона передаточных функций

Если сравнить матрицу передаточных функций и полученные разгонные характеристики(рисунок ), видно, что Кр из матрицы передаточных функций совпадают с Кр на графиках, можно сделать вывод: построение модели и преобразование выполнены верно.

4. Синтез многомерного ПИ-регулятора

Для синтеза ПИ-регулятора полученные матрицы должны быть расширены в матрицы A1, B1, C1:

A1=[Ad zeros(8,2); C eye(2)];

B1=[Bd;zeros(10)];

C1=[C eye(2)];

Матрицы параметров регулятора должны быть рассчитаны с помощью функции dlqr.

K=dlqr(A1,B1,Q,R)

L=dlqr(A1',C1',Q1,R1)'

Расширены матрицы имеют вид:

A1 =

Columns 1 through 12

0.9941 0 0 0 0 0 0 0 0 0 0 0

0.0258 0.9741 0 0 0 0 0 0 0 0 0 0

0.0025 0.1878 0.9048 0 0 0 0 0 0 0 0 0

0 0 0 0.9995 0 0 0 0 0 0 0 0

0 0 0 0.0347 0.9827 0 0 0 0 0 0 0

0 0 0 0 0 0.9941 0 0 0 0 0 0

0 0 0 0 0 0.0258 0.9741 0 0 0 0 0

0 0 0 0 0 -0.0025 -0.1878 0.9048 0 0 0 0

0 0 0 0 0 0 0 0 0.9941 0 0 0

0 0 0 0 0 0 0 0 0.0258 0.9741 0 0

0 0 0 0 0 0 0 0 0.0025 0.1878 0.9048 0

0 0 0 0 0 0 0 0 0 0 0 0.9984