6,63

7,37

8,07

9,22

Практическая реализация данного метода изложена в приложении 1.

Полученный результат представлен на рисунке 3.

2 ЭКСПОНЕНЦИАЛЬНЫЙ ФИЛЬТР

В аналоговом варианте экспоненциальный фильтр представляет собой апериодическое звено и описывается дифференциальным уравнением

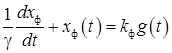, (6)

где и – параметры настройки фильтра.

Уравнению (6) соответствует амплитудно-фазовая характеристика (АФХ)

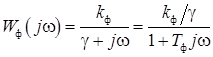, (7)

где 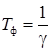– постоянная времени фильтра.

Из условия (математическое ожидание) для статического режима определяют оптимальное значение параметра . Коэффициент усиления

. (8)

Определение оптимального значения параметра производится из условия (4) (среднеквадратичная погрешность оценки).

Для этого предварительно рассчитывают спектральную плотность погрешности экспоненциального фильтра.

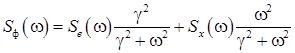. (9)

Дисперсия погрешности экспоненциального фильтра, равна

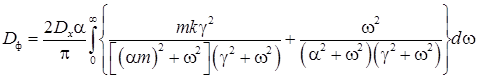. (10)

При вычислении этого интеграла оба слагаемых подынтегрального выражения раскладывают на простые дроби, каждая из которых сводится к табличному интегралу вида

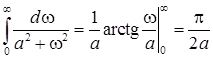. (11)

После выполнения соответствующих преобразований получают следующее выражение для дисперсии погрешности фильтрации:

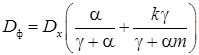. (12)

Оптимальное значение параметра настройки получают из необходимого условия экстремума функции :

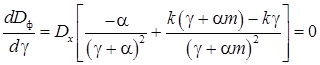. (13)

Откуда оптимальное значение параметра

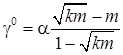. (14)

Таким образом, функция имеет единственную точку стационарности, тип которой зависит от знака второй производной при .