Курсовая работа: Численное интегрирование методом Гаусса
eps: =1e-4;
equateit(aaa,bbb,eps);
end;
2: begin
inputnum('a',aaa,0,1000);
inputnum('b',bbb,-1000,1000);
inputnum('k',kkk,-1000,1000);
inputnum('точность',eps,0.000000001,1);
equateit(aaa,bbb,eps);
end;
end;
until sel=0;
end.
3.5 Распечатка исходных данных и результатов решения контрольного примера
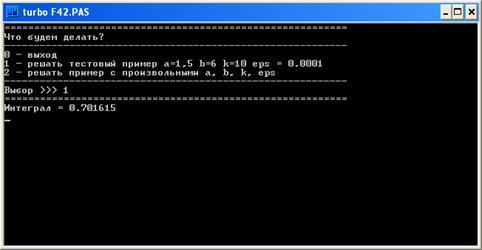
Заключение
В данной работе описана и реализована с помощью блок-схем и языка программирования TurboPascal задача нахождения численного решения интеграла методом Гаусса. Программное средство содержит средства вычисления интеграла по исходным данным, а также выбирая произвольный интервал и шаг интегрирования с заданной точностью. При этом на экран выводится график, отражающий процесс интегрирования заданной функции по шагам.
Представленный метод и реализованный алгоритм достаточно прост и эффективен для решения большого класса задач.
Список использованной литературы
1. Малыхина М.П. Программирование на языке высокого уровня TurboPascal. – Спб.: БХВ-Петербург, 2006, 544 с.
2. Немнюгин С.А. TurboPascal. – Спб.: Питер, 2002. – 496 с.
3. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: Нолидж, 1997. – 616 с.
4. Гусева А.И. Учимся программировать: PASCAL 7.0. Задачи и методы их решения. – М.: Диалог-МИФИ, 1997. – 256 с.
5. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ: Справочник. - М.: Наука. Гл. ред. физ. -мат. лит., 1987. – 240 с.
6. Сапаров В.Е., Максимов Н.А. Системы стандартов в электросвязи и радиоэлектронике: Учебное пособие для вузов. – М. - Радио и связь, 1985. – 248 с.
7. ГОСТ 19.701-90 (ИСО 5807-85). “Единая система программной документации. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения”/ Cб. ЕСПД. – М.: Изд-во стандартов, 1996. – 157 с.
8. Бахвалов Н., Жидков Н., Кобельков Г. Численные методы. М.: Лаборатория базовых знаний, 2001.632 с.
9. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений / Пер. с англ. М.: Мир, 1980.177с.
10. Самарский А.А., Гулин А.В. Численные методы: Учебное пособие для ВУЗов. М.: Наука, 1989.432с.