Курсовая работа: Численное решение системы линейных алгебраических уравнений методом Гаусса

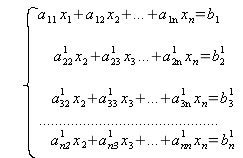(4)

Потом x2 из 3-го,..., n-го умножением второго уравнения на - a¹32/a¹22, - a¹42/a¹22,..., - a¹n2/a¹22 и сложением с 3,4,. n уравнениями.

И дальше по аналогии система приводится к треугольному виду:

.

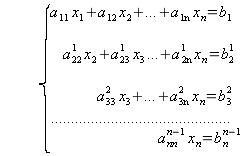Процесс приведения системы к треугольному виду называется прямым ходом. Общие формулы для прямого хода:

,

,

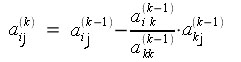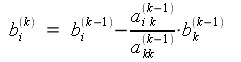где k =1,...,n - 1; i,j = k+1,...,n.

Для нахождения решения теперь необходимо вычислить неизвестные, начиная с n-го уравнения. Процесс вычисления значений неизвестных называется обратным ходом.

На каждом этапе xk находится по формуле

,

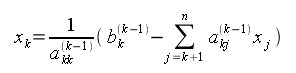где k = n, n-1,...,

3. Функциональные модели и блок-схемы решения задачи

Функциональные модели и блок-схемы решения задачи представлены на рисунках 1 и 2.

Условные обозначения:

I, J- временные переменные;

A- временная матрица;

B- массив свободных членов матрицы;

X- массив решений;

NUMB- временная переменная;

MATRIX- матрица для расчета;

ROW_COL, R_C, LEN- количество строк и столбцов в матрице;

ARRAY_B- рабочий массив свободных членов.

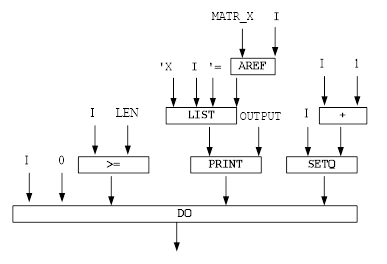
Рисунок 1 - Функциональная модель решения задачи для функции PRINT_RES

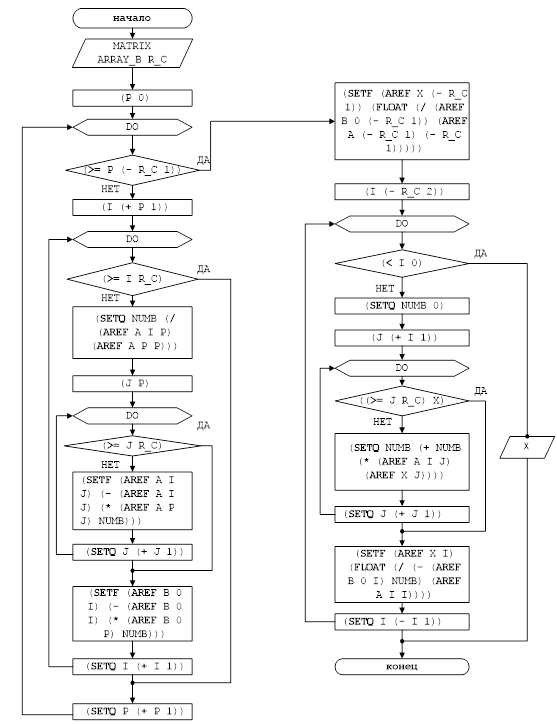
Рисунок 2 - Блок-схема решения задачи для функции METHOD_GAUS

4. Программная реализация решения задачи

; ROW_COL - КОЛИЧЕСТВО СТРОК И СТОЛБЦОВ МАТРИЦЫ

( SETQ ROW_COL 0)

(SETQ INPUT (OPEN " D: \MATRIX. TXT": DIRECTION: INPUT))