Курсовая работа: Численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу
Будем считать, что D = det A ¹ 0 т.е. решение существует и единственно.
Рассмотрим вначале прямые методы. В явном виде решение системы (1) записывается в виде формул Крамера
xi = Di /D
где Di - определитель матрицы, которая получается из матрицы A путем замены i-того столбца на столбец правых частей.
Этот метод очень неэкономичен так как для его применения требуется (n+1)! операций, поэтому на практике используются различные варианты метода исключения переменных (Гаусса). Метод исключения переменных состоит из двух этапов: прямого хода, заключающегося в преобразовании исходной системы к системе с треугольной матрицей коэффициентов, и обратного хода, т.е. решения системы с треугольной матрицей.
Пример 1. Решить следующую систему с помощью метода исключения Гаусса с выбором главного элемента по столбцу:
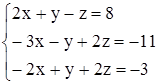 .
.
Решение:
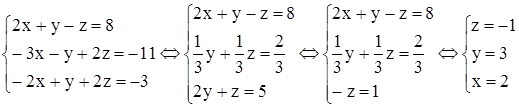 .
.
Пример 2. Решить следующую систему с помощью метода исключения Гаусса с выбором главного элемента по столбцу:
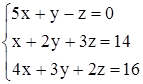 .
.
Составим расширенную матрицу системы.
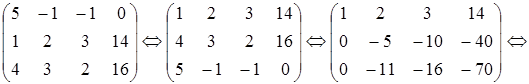
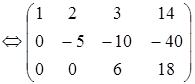 .
.
Решением системы являются:x =1, y = 2, z = 3.
2 Математические и алгоритмические основы решения задачи
2.1 Схема единственного деления
Рассмотрим сначала простейший вариант метода Гаусса, называемый схемой единственного деления.
2.1.1 Прямой ход
Прямой ход состоит из n - 1 шагов исключения.
1-й шаг. Целью этого шага является исключение неизвестного x1 из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a11 = 0. Будем называть его главным элементом 1-го шага.
Найдем величины
qi1 = ai1/a11 (i = 2, 3, …, n),
называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, n-го уравнений системы первое уравнение, умноженное соответственно на q21, q31, qn1. Это позволит обратить в нуль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему
a11x1 + a12x2 + a13x3 + … + a1nxn = b1 ,
a22(1)x2 + a23(1)x3 + … + a2n(1)xn = b2(1) ,
a32(1)x2 + a33(1)x3 + … + a3n(1)xn = b3(1) ,
an2(1)x2 + an3(1)x3 + … + ann(1)xn = bn(1) .
в которой aij(1) и bij(1) вычисляются по формулам