Курсовая работа: Численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу

В методе Гаусса с выбором главного элемента по столбцу гарантируется, что

|qik| ≤ 1 для всех k = 1, 2, …, n – 1 и i = k + 1, …, n.

Отличие этого варианта метода Гаусса от схемы единственного деления заключается в том, что на k-м шаге исключения в качестве главного элемента выбирают максимальный по модулю коэффициент aikk при неизвестной xk в уравнениях с номерами i = k + 1, …, n. Затем соответствующее выбранному коэффициенту уравнение с номером ik меняют местами с k-м уравнением системы для того, чтобы главный элемент занял место коэффициента akk(k-1). После этой перестановки исключение неизвестного xk производят, как в схеме единственного деления.

3 Функциональные модели и блок-схемы решения задачи

Блок-схема решения задачи представлена на рисунке 1.

Условные обозначения:

· K – размерность матрицы;

· MATRIX – матрица;

· N – размерность матрицы;

· X – матрица решения СЛАУ;

· I_MAX – индекс максимального элемента в строке;

· J_MAX – индекс максимального элемента в столбце;

· OTV – массив позиций элементов;

· RES – вспомогательный массив;

· TEMP – временная переменная;

· GLAV_EL – функция, определяющая на какой позиции должен стоять главный элемент;

· INDEX – рабочая переменная.

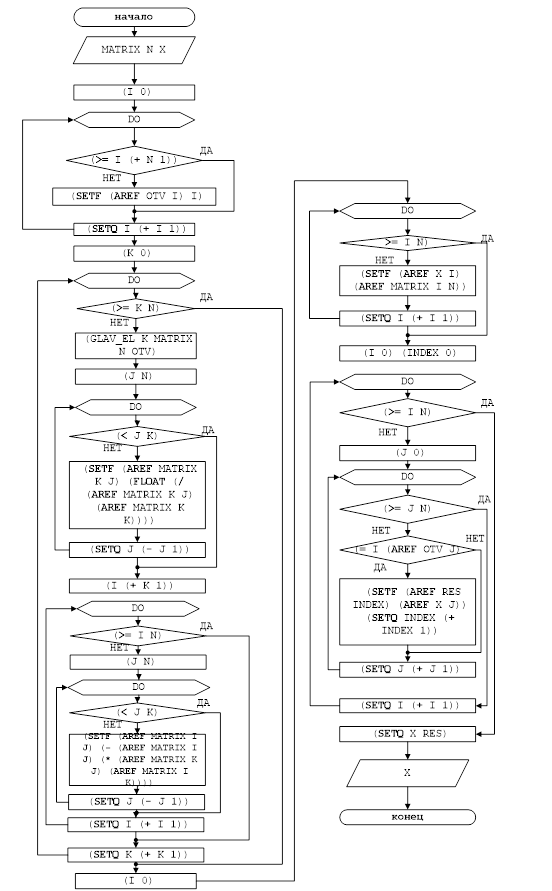
Рисунок 1 – Блок-схема решения задачи для функции GAUSS

\

4 Программная реализация решения задачи

ФУНКЦИЯ ПОИСКА МАКСИМАЛЬНОГО ЭЛЕМЕНТА И ПЕРЕСТАНОВКИ СТРОК И СТОЛБЦОВ

(DEFUN GLAV_EL (K MATRIX N X)

(DECLARE (SPECIAL I_MAX))

(DECLARE (SPECIAL J_MAX))

(DECLARE (SPECIAL TEMP))

(DECLARE (SPECIAL I))

(SETQ I_MAX K)

(SETQ J_MAX K)