Курсовая работа: Дидактичний експеримент у трудовому навчанні
Якщо ми знаємо значення випадкових величин та імовірність їх появи, то можна припустити, що нам відомий закон розподілу цих випадкових величин. Закон розподілу здебільшого записують у формі таблиці, яку називають ще рядом розподілу випадкової величини. Наприклад, візьмемо клас, де 50 учнів провели контрольну роботу; її результатом стали оцінки з відповідною частотою повторення (таб.1).
Таблиця 1
Таблиця розподілу випадкових величин
| Оцінка Хі | Частота повторення Fi (m) |
| 1 2 3 4 5 | 4 8 21 12 5 |
На основі результатів контрольної роботи визначимо частку оцінки "3" від загальної кількості оцінок. Для цього скористаємось формулою 1.2:
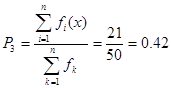або42 %
Це означає, що оцінка "3" зустрічається майже в кожному другому випадку за цією контрольною роботою.
Доцільно зазначити, що ряд розподілу, зображений у табл.1, можна також подати графічно. З цією метою на осі абсцис треба відкласти значення величини (оцінки), а на осі ординат - частоту появи величини (кількість оцінок). У результаті утворюється многокутник, який називають полігоном частоти (мал.1). У ньому частота інтервалу віднесена до його центра (що зображено точками).
Якщо частоти зобразити рівномірно по всьому інтервалу, то можна одержати гістограму (мал.2).
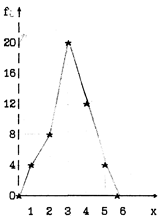
Мал.1. Полігон частоти. Мал.2. Гістограма.
Властивості одержаного розподілу характеризують відповідними статистиками: середньою арифметичною величиною, середнім квадратичним відхиленням, модою, медіаною тощо.
Середня арифметична величина характеризує середній рівень значення випадкової величини в конкретних випадках і обчислюється за формулою:
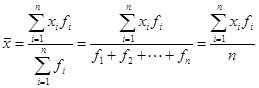
де Хі - величина окремих елементів певної сукупності;
fі - частота появи окремої величини;
n - кількість членів сукупності (об'єм сукупності).
У нашому випадку (див. дані табл. 1):
Середнє квадратичне відхилення характеризує розсіювання в дослідженні значення випадкової величини навколо її середнього арифметичного. Середнє квадратичне відхилення обчислюють за формулою:
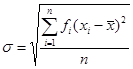
- середнє квадратичне відхилення;
- величина окремих елементів сукупності;
- середня арифметична величина;
n - кількість членів сукупності.
У нашому випадку (див. дані табл. 1)
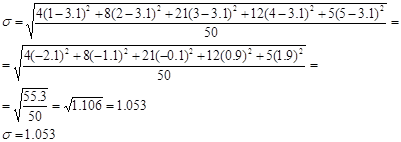
Величину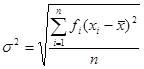 
(квадрат середнього квадратичного відхилення) називають дисперсією.
Медіана - середній член упорядкованого розподілу частоти, по обидва боки від якого залишається однакова кількість членів.
Мода. - значення в статистичному розподілі частоти подій, яке повторюється найчастіше.