Курсовая работа: Дослідження чисельних методів інтегрування
В методах Монте-Карло вузли вибираються за допомогою датчика випадкових чисел, відповідь носить ймовірний характер. Методи виявляються ефективними при обчисленні великої кратності.
2. Алгоритми методів
Для обчислення інтегралу за формулою Сімпсона потрібно спочатку розбити проміжок інтегрування x є (a,b) на рівні інтервали величиною h (крок інтегрування), потім знаходять вузли інтерполяції xi за формулою
xi=xi-1+h або xi=x0+ih=a+ih,
після чого підставляють отримані значення у формулу (3). В кінці оцінюють похибку. У додатку А приведено алгоритм методу Сімпсона.
Для обчислення значення інтегралу методом Чебишева обирають порядок методу n і знаходять значення ti. Після цього розбивають інтервал інтегрування на k проміжків і знаходять значення інтегралу для кожного проміжку (j=1,…,k), після чого сумують отримані значення
|
|
Значення абсцис xi всередині кожного інтервалу знаходять за формулою
xi=(aj+1+aj)/2+ti(aj+1-aj)/2,
де aj=a+ih, a0=a, ak=b.
Ij знаходять за формулою (1.5). В кінці оцінюють похибку. Алгоритм методу Чебишева приведено у додатку А.
3. Опис програми
3.1 Вибір інструментальних засобів
Для написання програми, яка обчислює інтеграли заданими методами, було обрано компілятор Тurbo C++. Даний компілятор був обраний тому, що мова програмування C++ дуже проста і в той же час сам компілятор являється потужною сучасною системою програмування. Найважливішим аргументом для вибору даного компілятора, є тип дійсних чисел extended, який має дуже високу точність (до 19 цифри), якої немає в жодному іншому широковживаному компіляторі. Так як різниця між деякими числами, отриманими в результаті роботи програми, дуже мала і іноді помітна починаючи з дев’ятого знаку, то стає очевидним що потрібна точність саме такого порядку.
3.2 Вхідні та вихідні дані
Для розробленої програми вхідними даними є межі інтегрування a та b, а також множники біля змінної інтегрування x, c та d. Всі дані мають тип extended.
Вихідними даними являється чисельне значення інтегралу, обчислене методами Трапеції та Чебишева, причому кожним методом інтеграл обчислюється з 3 кроками. Також вихідними даними являються похибки, обчислені для кожного знайденого значення.
3.3 Структура програми
Програма, написана для вирішення поставленої задачі, містить кілька підпрограм. Спочатку програма виводить загальні відомості про своє призначення, потім пропонує змінити деякі параметри, після чого виконує обчислення інтегралу згаданими вище методами з кроками 0.1, 0.2 та 0.5. Підінтегральна функція для зручності міститься у функції f. Для обчислення інтегралу методом Сімпсона використовується функція Simpson, що приймає в якості параметрів межі інтегрування та крок обчислення. Для обчислення інтегралу методом Чебишева використовується дві функції: Chebushev та difChebushev. Функція Chebushev викликається безпосередньо з основної програми. Вона ділить межі інтегрування на проміжки, за величиною рівні кроку h, викликає функцію difChebushev для обчислення інтегралу на кожному проміжку, після чого сумує отримані значення, вираховуючи значення інтегралу. Потім основна програма виводить отримані значення на монітор, після чого для кожного значення вираховує похибку і виводить її на монітор.
Блок-схему програми наведено в додатку Б.
3.4 Інструкція користувачеві
Для запуску програми необхідно запустити на виконання файл program.exe.
Розроблена програма інтуїтивно зрозуміла користувачеві. Перша дія, яку потрібно виконати користувачеві – проглянути параметрі та при необхідності в момент, коли програма запропонує змінити деякі параметри, натиснути клавішу ‘Y’ та ввести потрібні значення параметрів. Після цього програма виводить на монітор обчислені значення інтегралу. Користувачеві потрібно лише використати ці значення в своїх цілях. В кінці програма пропонує або вихід, або перезавантаження для повторного розрахунку. Якщо користувачеві потрібно обчислити ще один інтеграл, необхідно натиснути клавішу ‘R’.
4. Аналіз результатів розрахунку
Як видно з похибок програма дає досить точні результати обчислень. Отримані дані підтверджують, що обчислення методом Чебишева дають результат, який за точністю на кілька порядків перевищує точність методу Трапеції. Значення інтегралу, обчисленого за допомогою програми Mathcad, рівне – 2,681.
Нижче наведено результат роботи програми.
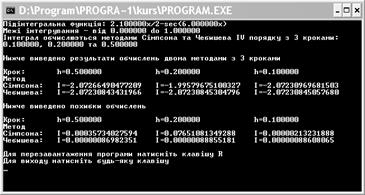
Висновки
В ході виконання даної курсової роботи було розглянуто методи чисельного інтегрування, а саме: Чебишева та Трапеції. Було досліджено вказані методи інтегрування та порівняно їх точності, розроблено програму на компіляторі Turbo C++, яка знаходить чисельне значення вказаного інтегралу. Таким чином були набуті практичні навички програмування задач, які ставить курс «Обчислювальні методи та застосування ЕОМ».
Література
1. Квєтний Р.Н. Методи Комп’ютерних обчислень. - Навчальний посібник. - Вінниця: ВДТУ, 2001. - с. 92
2. Волков Е. А. Численные методы. - М.: Наука, 1982. - с. 102.
3. Самарский А.А., Гулин А.В. Численные методы. - М: Наука, 1989. - с. 161.
4. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. - Численные методы. - М: Наука, 1987. - с. 83
Додатки
Додаток А
Алгоритми методів
Алгоритм методу Сімпсона