Курсовая работа: Дзета функция Римана

, а и . Отсюда, подставляя в двойное неравенство, имеем

(3). В левом неравенстве положим n =0, тогда , то есть . В правом же возьмём n =1 и получим , далее , и, наконец, . Переходя в неравенствах к пределу при , находим .

Отсюда, в частности, следует, что . Действительно, положим . Тогда , то есть . Поэтому . Из того, что , а , вытекает доказываемое утверждение.

Можно, однако, получить ещё более точный результат для оценки поведения дзета-функции в окрестности единицы, чем приведённые выше, принадлежащий Дирихле. Будем отталкиваться от очевидного при произвольном n равенства . Прибавим ко всем частям неравенств (3) сумму и вычтем . Имеем . Пусть здесь s стремится к единице. По правилу Лопиталя легко вычислить и . Мы пока не знаем, существует ли предел выражения при , поэтому, воспользовавшись наибольшим и наименьшим пределами, напишем неравенства так:

. Ввиду произвольности n возьмём . Первое и последнее выражения стремятся к эйлеровой постоянной C (C0,577). Значит , а, следовательно, существует и обычный предел и .

Найденные выше пределы позволяют получить лишь приблизительное представление о виде графика дзета-функции. Сейчас мы выведем формулу, которая даст возможность нанести на координатную плоскость конкретные точки, а именно, определим значения , где k – натуральное число.

Возьмём известное разложение , где - знаменитые числа Бернулли (по сути, через него эти числа и определяются). Перенесём слагаемое в левую часть равенства. Слева получаем cth, а в правой части - , то есть cth. Заменяем на , получаем cth.

С другой стороны, существует равенство cth, из которого cth. Подстановкой вместо находим cth. Если , то для любого N 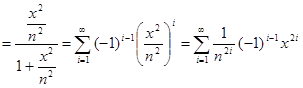и по теореме о сложении бесконечного множества степенных рядов cth.

Приравняем полученные разложения:

, следовательно . Отсюда немедленно следует искомая формула

(4), где - k -е число Бернулли. Она удобна тем, что эти числа хорошо изучены и для них составлены обширные таблицы.

Теперь, исходя из полученных результатов, можно построить эскиз графика дзета-функции Римана, достаточно хорошо отражающий её поведение на всей области определения.

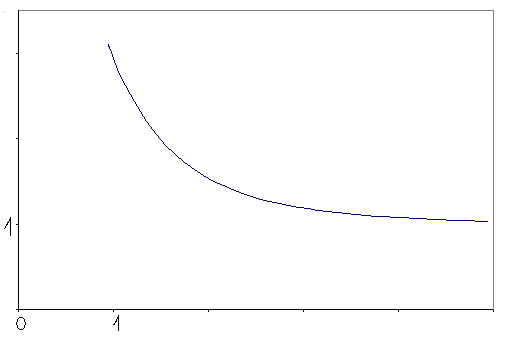
Леонард Эйлер, впервые рассмотревший дзета-функцию, получил замечательное разложение её в бесконечное произведение, которое иногда тоже принимают за определение:

, где p_i – i -е простое число (4).

Докажем тождественность ряда (1) и произведения (4). Вспомнив формулу суммы геометрической прогрессии, получаем равенство

Если перемножить конечное число таких рядов, отвечающих всем простым числам, не превосходящим заданного натурального числа N , то получившееся частичное произведение окажется равным 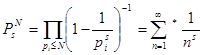, где символ * означает, что суммирование распространяется не на все натуральные числа, а лишь на те из них (не считая единицы), которые в своём разложении содержат только простые числа меньшие N . Так как первые N натуральных чисел этим свойством обладают, то

(5).

Сумма содержит не все числа, большие N +1, поэтому, очевидно, . Из (5) получаем

(6).

Ввиду сходимости ряда (1), выражение справа, представляющее его остаток после N -го члена, стремится к нулю при N стремящимся к бесконечности, а есть произведение (4). Значит из неравенства при , что и требовалось доказать.

Формула (4) важна потому, что она связывает натуральный ряд, представленный множеством значений аргумента дзета-функции, со множеством простых чисел. Ещё один шаг в этом направлении мы сделаем, оценив , а именно показав, что , где остаётся ограниченным при .

Из (4) следует, что 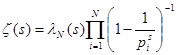, где N , а при . Возьмём логарифм от обеих частей равенства, тогда . Натуральные логарифмы под знаком суммы разлагаются в ряд: . Подставив полученные разложения в равенство и устремив N к бесконечности, имеем . Остаётся доказать ограниченность последнего слагаемого. Ясно, что . Последнее равенство справедливо, так как . Далее, очевидно, , что и завершает доказательство.

На этом закончим изложение свойств дзета-функции Римана для действительного аргумента, так как наибольший теоретический и прикладной интерес представляет случай изложенный во второй главе.

Глава 2.

Все результаты первой главы, касающиеся дзета-функции Римана, были получены в предположении, что её аргумент s – действительное число. Однако, самые выдающиеся исследования и многочисленные важные приложения стали возможны лишь после включения в область определения функции комплексных чисел. Впервые рассмотрел дзета-функцию как функцию мнимого аргумента немецкий математик Бернгард Риман, глубоко изучивший её свойства и широко применявший её в теории чисел. В честь него функция получила своё название.

Для комплексной дзета-функции остаётся в силе определение, данное в главе 1, с тем лишь изменением, что теперь там будет C . Возникает необходимость найти новую область определения. С этой целью докажем следующее утверждение: в полуплоскости ( действительная часть числа x ) ряд

(1) сходится абсолютно.

Пусть . Подсчитаем абсолютные величины членов ряда (1), . Первый множитель содержит только вещественные числа и , так как . Ко второму же множителю применим знаменитую формулу Эйлера, получим . Значит, . Ввиду сходимости ряда при α>1, имеем абсолютную сходимость ряда (1).

На своей области определения дзета-функция аналитична. Действительно, при всяком q >0 и фиксированном α>1+q , числовой ряд мажорирует ряд из абсолютных величин , где , откуда, по теореме Вейерштрасса, следует равномерная сходимость ряда в полуплоскости . Сумма же равномерно сходящегося ряда из аналитических функций сама является аналитической функцией.