Курсовая работа: Дзета функция Римана

В связи с этим замечанием становится возможным использовать разложение дзета-функции в произведение , где s теперь любое комплексное число, такое, что . Применим его к доказательству отсутствия у функции корней.

Оценим величину , используя свойство модуля : , где как обычно . Так как , то , а , следовательно, дзета-функция в нуль не обращается.

Вопрос о нулях дзета-функции, а также другие прикладные вопросы получают новые широкие возможности для исследования, если распространить её на всю комплексную плоскость. Поэтому, сейчас мы одним из многих возможных способов найдём аналитическое продолжение дзета-функции и выведем её функциональное уравнение, характеризующее и однозначно определяющее .

Для этого нам понадобится формула

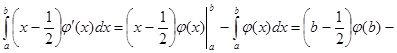
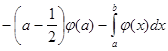(2), которая выводится следующим образом. Используя свойства интегралов можно записать . Для любого d при , значит и , а . . Следовательно, . Интеграл можно найти интегрированием по частям, принимая , ; тогда , а . В результате . Вычтем из этого интеграла предыдущий и получим 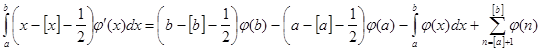, отсюда легко следует равенство (2).

Теперь положим в (2) , , a и b – целые положительные числа. Тогда 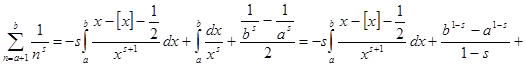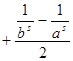. Пусть сначала , примем a =1, а b устремим к бесконечности. Получим 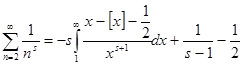. Прибавим по единице в обе части равенств:

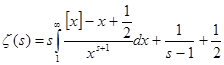(3).

Выражение является ограниченным, так как , а функция абсолютно интегрируема на промежутке при , то есть при , . Значит, интеграл 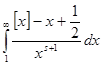абсолютно сходится при , причём равномерно в любой конечной области, лежащей в комплексной плоскости справа от прямой . Тем самым он определяет аналитическую функцию переменной s , регулярную при . Поэтому правая часть равенства (3) представляет собой аналитическое продолжение дзета-функции на полуплоскость и имеет там лишь один простой полюс в точке с вычетом, равным единице.

Для можно преобразовать выражение (3) дзета-функции. При имеем , значит, и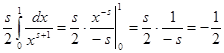. Теперь при (3) может быть записано в виде .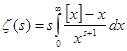

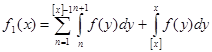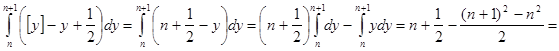
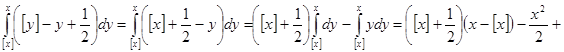
Немного более сложными рассуждениями можно установить, что в действительности (3) даёт аналитическое продолжение дзета-функции на полуплоскость . Положим , а , то есть первообразная для . ограничена, так как , а интеграл и ограничен из-за того, что . Рассмотрим интеграл 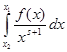при x ₁ >x ₂ и . Проинтегрируем его по частям, приняв , , тогда , а по указанному выше утверждению . Получаем 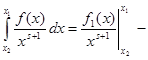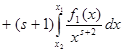. Возьмём , а . Имеем , , потому что является ограниченной функцией. Значит,

(4).

Пользуясь абсолютной сходимостью интеграла , если , и ограниченностью функции , делаем вывод, что в левой части равенства (4) интеграл тоже сходится при . Значит формулой (3) можно продолжить дзета-функцию и на полуплоскость правее прямой .

Нетрудно установить, что для отрицательных , поэтому из (3) имеем

(5) при .

Из теории рядов Фурье известно, что для нецелых значений x справедливо разложение в ряд

(6).

Подставим его в равенство (5) и проинтегрируем ряд почленно:

. Сделаем в полученном интеграле подстановку , отсюда следует , а , и получим далее . Известно, что , значит . Из известного соотношения для гамма-функции , по формуле дополнения , следовательно

Итак, мы получили функциональное уравнение дзета-функции Римана

(7),

которое само по себе может служить средством изучения этой функции, так как вполне характеризует её, в том смысле, что любая другая функция , удовлетворяющая равенству (7), а также ещё некоторым естественным условиям, тождественна с .

Пока, правда, как следует из рассуждений, мы доказали формулу (7) для . Однако правая часть этого равенства является аналитической функцией s и при . Это показывает, что дзета-функция может быть аналитически продолжена на всю комплексную плоскость, причём не имеет на ней никаких особенностей, кроме упоминавшегося полюса при .

Чтобы доказательство было строгим, мы должны ещё обосновать почленное интегрирование. Поскольку ряд (6) сходится почти всюду и его частичные суммы остаются ограниченными, почленное интегрирование на любом конечном отрезке допустимо. Ввиду для любого , остаётся доказать, что при . Но интегрируя внутренний интеграл по частям имеем

. Отсюда без труда получается наше утверждение.

Функциональное уравнение дзета-функции (7) может быть записано многими способами. Например, заменим s на 1-s , получаем равносильное равенство

(8). Из него можно получить два небольших следствия.

Подставим в (8) вместо s число 2m , где m – натуральное число. Имеем . По формуле (4) первой главы , а , поэтому и произведя в правой части все сокращения, учитывая, что , получим .

Покажем ещё, что . Для этого прологарифмируем равенство (8): и результат продифференцируем . В окрестности точки s =1 , , , где С – постоянная Эйлера, а k – произвольная постоянная. Следовательно, устремляя s к единице, получим , то есть . Опять из формулы (4) главы 1 при k =0 , значит, действительно, .

Глава 3.

Как уже было сказано, дзета-функция Римана широко применяется в математическом анализе. Однако наиболее полно важность её выявляется в теории чисел, где она оказывает неоценимую помощь в изучении распределения простых чисел в натуральном ряду. К сожалению, рассказ о серьезных и нетривиальных применениях дзета-функции Римана выходит за рамки этой работы. Но чтобы хотя бы немного представить мощь этой функции, докажем с её помощью несколько интересных утверждений.