Курсовая работа: Дзета функция Римана

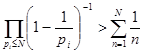Другое доказательство этого факта, использующее дзета-функцию, было дано Эйлером. Рассмотрим данное в первой главе равенство (5) при s =1, получим , отсюда и ввиду расходимости гармонического ряда, имеем при

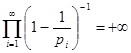(1). Если бы количество простых чисел было конечным, то и это произведение имело конечное значение. Однако, полученный результат свидетельствует об обратном. Доказательство завершено.

Теперь перепишем (1) в виде 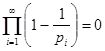. Опираясь на теорему о сходимости бесконечного произведения, из расходимости предыдущего делаем вывод, что ряд расходится. Это предложение даёт некоторую характеристику роста простых чисел. Подчеркнём, что оно гораздо сильнее утверждения о расходимости гармонического ряда, так как здесь речь идёт лишь о части его членов, тем более что в натуральном ряде имеются сколь угодно длинные промежутки без простых чисел, например: , , … , .

Несмотря на свою простоту приведённые выше предложения важны в концептуальном плане, так как они начинают череду исследований всё более и более глубоких свойств ряда простых чисел, которая продолжается по сей день. Первоначально, основной целью изучения дзета-функции как раз и было исследование функции , то есть количества простых чисел не превосходящих x . В качестве примера формулы, связывающей и , мы сейчас получим равенство

(2).

Сначала воспользуемся разложением дзета-функции в произведение: 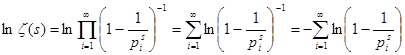. Из логарифмического ряда , учитывая, что 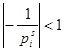, приходим к ряду 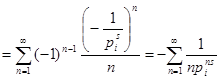. Значит, .

Теперь вычислим интеграл в правой части (2). Так как при , то 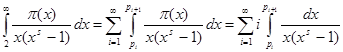. Во внутреннем интеграле положим , тогда и 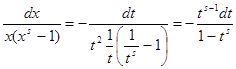, отсюда 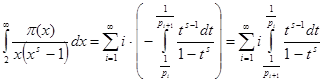.В промежутке интегрирования , поэтому верно разложение и . Получаем 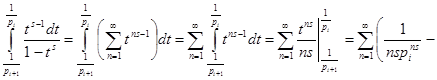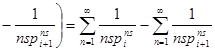. Теперь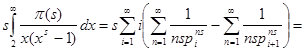 . Если сравнить полученное значение интеграла с рядом для , то увидим, что они тождественны и равенство (2) доказано.

Используем формулу (2) для доказательства одной очень серьёзной и важной теоремы, а именно получим асимптотический закон распределения простых чисел, то есть покажем, что .

В качестве исторической справки отмечу, что великий немецкий математик Карл Фридрих Гаусс эмпирически установил эту закономерность ещё в пятнадцатилетнем возрасте, когда ему подарили сборник математических таблиц, содержащий таблицу простых чисел и таблицу натуральных логарифмов.

Для доказательства возьмём формулу (2) и попытаемся разрешить это уравнение относительно , то есть обратить интеграл. Сделаем это с помощью формулы обращения Меллина следующим образом. Пусть . Тогда

(3). Этот интеграл имеет нужную форму, а не повлияет на асимптотику . Действительно, так как , интеграл для сходится равномерно в полуплоскости , что легко обнаруживается сравнением с интегралом 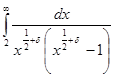. Следовательно, регулярна и ограничена в полуплоскости . То же самое справедливо и относительно , так как .

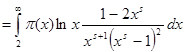Мы могли бы уже применить ф