Курсовая работа: Эффект поля. Расчёт эффективной подвижности носителей заряда
Qs – связанный заряд на поверхностных уровнях
Гp и Гn – полные количества избыточных дырок и электронов, определяемые формулой (1.3)


Кроме того, имеется ещё заряд, создаваемый ионами в объеме полупроводника (заряженными донорами и акцепторами), и ионами, адсорбированными на внешней поверхности окисла. В отсутствие внешнего поля заряд ионов равен по величине и противоположен по знаку заряду Q.
Во многих случаях можно считать, что в эффекте поля ионный заряд не изменяется. Это справедливо, если доноры и акцепторы в объеме полупроводника полностью ионизированы. Адсорбированные же ионы обмениваются электронами с полупроводником очень медленно (часто за многие секунды и минуты), и за время измерения их заряд остается постоянным. Поэтому индуцированный заряд равен
δQ = δQv + δQs = e( δГp – δГn ) + δQs (1.4)
Так как Гp и Гn – известные функции поверхностного потенциала Ys , а этот последний тоже определяется из эффекта поля, то величину δQv можно легко найти. С другой стороны, суммарный индуцированный заряд (отнесенный к единице площади) равен
δQ = Cu (1.5)
где С – емкость конденсатора на единицу площади, которая непосредственно определяется на опыте. Поэтому оказывается возможным определить δQs и найти, какая доля иногда выражают с помощью эффективной подвижности. Она, по определению, равна
(1.6)
где δG – изменение проводимости в эффекте поля.
Эта величина имеет особенно простой физический смысл, если искривление зон невелико и проводимость везде можно считать монополярной. Тогда получаем для дырочного полупроводника
![]() ,(1.7)
,(1.7)
а следовательно,
В этом случае μэф определяет, какая доля полного заряда поверхности находится в подвижном состоянии.
Исследуя зависимость Qs от Ys , можно определить энергетическое положение поверхностных уровней энергии и их концентрацию. Действительно, при изменении Ys поверхностные уровни, так же как и края зон у поверхности, перемещаются относительно уровня Ферми F. При прохождении какого-либо уровня Es через F зарядное состояние уровня изменяется. При наличии уровней только одного типа это проявляется на кривых зависимости Qs от Ys возникновением ступени.
Чтобы охарактеризовать энергетический спектр поверхностных состояний, отсчитываем Es при неискривленных зонах (Ys =0) от положения уровня Ферми в собственном полупроводнике Fi , обозначая εs ≡ Es – Ei . Тогда
Es – F = εs – (F – Fi ) – kTYs .
Для невырожденных (в объеме ) полупроводников получаем
![]()
Поэтому можно найти, что вероятность заполнения уровня Es при данном Ys есть

Если рассматриваемые уровни акцепторные и их поверхностная концентрация равна ν, то заряд поверхности буде равен
Qs = –eνf(εs , Ys ). (1.8)
Для донорных уровней получаем
Qv = eν(1 – f(εs , Ys )). (1.9)
Из формул (1.8) и (1.9) видно, что в обоих случаях на кривых зависимости Qs от Ys появляется ступень, а также точка перегиба. Последняя соответствует поверхностному потенциалу
![]()
Значит, определяя по данным эффекта поля Ys 1 , можно найти εs . Величина ступени равна eν.
В случае нескольких дискретных уровней энергии получилось бы не одна, а несколько точек перегиба.
Если имеется непрерывный энергетический спектр поверхностных состояний, то Q, получается суммированием выражений типа. Так, например, для акцепторных уровней получаем:
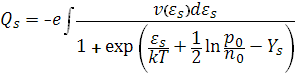
Где интегрирование производится по всей запрещенной зоне энергий. Здесь ν(εs ) есть поверхностная плотность уровней, рассчитанная на единичный интервал энергии. В этом случае задача определения энергетического спектра поверхностных состояний ν(εs ) по экспериментальной зависимости Qs от Ys становится гораздо более сложной и требует либо дополнительных данных, либо дополнительных предположений.