Курсовая работа: Эффект поля. Расчёт эффективной подвижности носителей заряда

Форма её зависит от степени однородности поверхности. Если свойства последней всюду одинаковы, то яма, очевидно, имеет вид желоба с острым дном, вытянутого вдоль поверхности. При достаточной глубине и ширине ямы в ней могут образоваться связанные состояния, находясь в которых, электроны локализованы вблизи поверхности. Это явление называется поверхностным квантованием. В одномерном случае указанным состояниям отвечали бы дискретные уровни в запрещенной зоне; в трехмерной задаче с однородной поверхностью получаем поверхностные энергетические зоны.

Вблизи границы раздела полупроводника с другой средой можно создать условия для реализации квантового размерного эффекта, ограничивая движение носителей в слое, толщина которого сравнима с их дебройлевской длиной волны. Так, если в полупроводнике p-типа, например, с помощью эффекта поля создать на поверхности достаточно большой изгиб зон вниз, то около границы раздела с диэлектриком в полупроводнике можно образовать узкий потенциальный желоб с размерно-квантовыми электронами (рисунок 1.7). Поскольку электроны «заквантованы» только в направлении х, то их спектр имеет вид двумерных подзон, а состояние определяется номером подзоны и двумерным квазиимпульсом с компонентами p_y , p_z . При достаточно низких температурах все электроны оказываются в самой нижней подзоне и образуют двумерный электронный газ.

Аналогичная ситуация имеет место в гетеропереходе GaAs – GaAl_x As_{1- x} ,

когда из специально легированного донорами полупроводника GaAl_x As_{1- x} с широкой запрещенной зоной электроны переходят в GaAs и образуют в нем около границы раздела канал с двумерным электронным газом. Благодаря селективному легированию и хорошему согласованию решеток компонент гетероперехода носители в двумерном канале обладают очень высокой подвижностью. На основе подобных структур созданы сверхбыстродействующие транзисторы.

Тонкий слой полупроводника, ограниченного с обеих сторон полупроводником с большей шириной запрещенной зоны, представляет собой кантовую яму (рисунок 1.8)

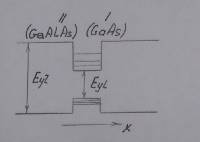
Рисунок 1.8 – Схематическое изображение квантовой ямы

А периодическая последовательность таких слоев образует макроскопическую квантовую сверхрешетку (рисунок 1.9)

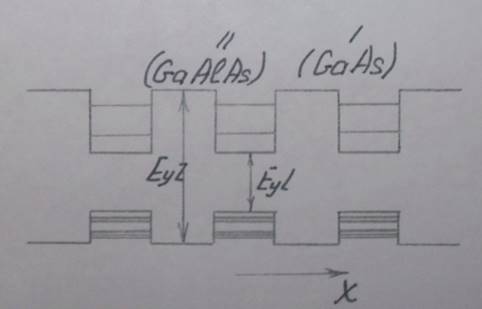
Рисунок 1.9 – Схематическое изображение сверхрешетки GaAs – GaAlAs

Реальные поверхности полупроводников, обработанные в травителе и находящиеся в атмосфере, обычно бывают покрыты аморфным и пористым слоем оксида толщиной (2 – 7) нм. Концентрация поверхностных состояний на таких поверхностях может быть порядка 10¹¹ – 10¹² см^-2 , т.е. значительно меньшей, чем концентрация на атомарно-чистых поверхностях. Это может быть связано с уменьшением концентрации собственных поверхностных состояний при окислении поверхности. Неоднородность поверхности приводит к тому, что полной аналогии между поверхностными и объемными зонами нет. Состояния в поверхностных зонах вблизи неоднородной поверхности или границы раздела могут оказаться локализованными не только вдоль оси Ох, но и в плоскости yz; в результате электропроводность по поверхностным зонам может не проявляться[1].

1.1 Зонная диаграмма

Будем считать, что электрическое поле создается заряженной металлической плоскостью с поверхностной плотностью зарядов σ. Поскольку силовые линии электрического поля должны быть замкнуты, то на поверхности полупроводника возникает равный по величине, но противоположный по знаку электрический заряд. В зависимости от знака заряда на металлической плоскости (положительной или отрицательной) экранирующий это поле заряд в приповерхностной области полупроводника также будет различных знаков. На рисунке 1.1.1 приведены ситуации положительно и отрицательно заряженной плоскости.

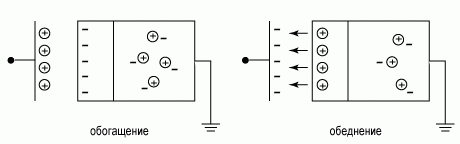
Рисунок 1.1.1 – Изменение концентрации свободных носителей в приповерхностной области полупроводника при наличии вблизи поверхности заряженной металлической плоскости

Случай, когда в приповерхностной области возрастает концентрация свободных носителей, носит название обогащение, а когда в приповерхностной области уменьшается концентрация свободных носителей - обеднение.

Если концентрация доноров в объеме полупроводника N_D =10¹⁵ см^-3 , то среднее расстояние между свободными электронами (и ионизированными донорами) в квазинейтральном объеме полупроводника будет равно, а = N_D ^-1/3 = 10^-5 см = 1000 Å. При поверхностной плотности заряда = 10¹² см^-2 толщина слоя пространственного заряда ионизованных доноров будет равна 10¹¹ / 10¹⁵ = 10^-4 см или 1 микрон. Отсюда следует, что электрическое поле в полупроводник может проникать на значительные расстояния.

Изменение концентрации свободных носителей в приповерхностной области полупроводника под действием внешнего электрического поля получило название эффекта поля.

При наличии внешнего поля приповерхностная область в полупроводнике не будет электронейтральной. Заряд, возникший в этой области, обычно называется пространственным зарядом, а сама область - областью пространственного заряда. Наличие электрического поля E(z) в области пространственного заряда меняет величину потенциальной энергии электрона. Если поле направлено от поверхности вглубь полупроводника, то электроны в этом случае будут иметь минимальную энергию у поверхности, что соответствует наличию потенциальной ямы для электронов там же.

Изменение потенциальной энергии электронов:

где U(∞)-потенциальная энергия электронов в квазинейтральном объеме полупроводника. Поскольку на дне зоны проводимости кинетическая энергия электронов равна нулю, то изменение потенциальной энергии по координате должно точно так же изменить энергетическое положение дна зоны проводимости E_c , (а соответственно и вершины валентной зоны E_v .) На зонных диаграммах это выражается в изгибе энергетических зон[5].

Величина разности потенциалов между квазинейтральным объемом и произвольной точкой ОПЗ получила название электростатического потенциала:

Значение электростатического потенциала на поверхности полупроводника называется поверхностным потенциалом и обозначается символом ψ_s .

Знак поверхностного потенциала ψ_s соответствует знаку заряда на металлическом электроде, вызывающего изгиб энергетических зон. ψ_s > 0, зоны изогнуты вниз, ψ_s < 0, зоны изогнуты вверх (рис. 11).

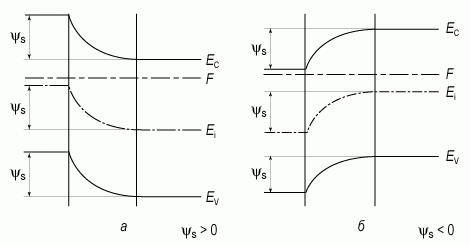
Рисунок 1.1.2 – Энергетические зоны на поверхности полупроводника n-типа:а) в случае обеднения; б) в случае обогащения

2 ЭФФЕКТ ПОЛЯ ПРИ РАЗЛИЧНЫХ ВЗАИМОДЕЙСТВИЯХ

2.1 Влияние квантово-размерных слоев In(Ga)As на эффект поля в слоях GaAs

Квантово-размерные гетеронаноструктуры (ГНС) с квантовыми точками (КТ) и квантовыми ямами (КЯ) In(Ga)As/GaAs играют важную роль в современной электронике. Исследование эффекта поля в этих структурах представляет интерес в связи с разработкой новых методик диагностики электронных параметров этих структур. При встраивании квантово-размерного слоя In(Ga)Asв приповерхностную область пространственного заряда (ОПЗ) матрицы GaAs эти слои должны проявлять себя в эффекте поля аналогично поверхностным состояниям (ПС) как электронные или дырочные ловушки для инжектированных носителей. В связи с конкуренцией квантово-размерных и поверхностных состояний за захват носителей высокая поверхностная концентрация поверхностных состояний в GaAs создает определенные трудности в выделении вклада квантово-размерных состояний на характеристиках эффекта поля. Для определения электронных параметров квантово-размерных слоев, в частности плотности состояний, высоты эмиссионного барьера и др., обычно используется емкостная диагностика барьеров Шоттки или p -n - переходов в квантово-размерных гетеронаноструктурах. В данной работе изучалась возможность использования эффекта поля для диагностики гетеронаноструктур In(Ga)As/GaAs.

2.1.1 Методика исследования

Исследовались гетеронаноструктуры с одиночными слоями квантовых точек InAsи квантовых ям In_0.2 Ga_0.8 As шириной 3 нм, встроенными в область пространственного заряда на разных расстояниях d_c = 5, 20, 100 и 300 нм от поверхности буферного слоя GaAsn -типа, который предварительно наносилсяна подложку полуизолирующего GaAs. Благодаря закреплению (пиннингу) уровня Ферми на поверхностных состояниях в приповерхностной области слоя n-GaAs возникает обедненный электронами слой с вы­сотой барьера около 0.6 эВ. Ширина области пространственного заряда при уровне легирования буферного слоя ~ 10¹⁶ см^-3 составляла обычно 200-250 нм. Из­менение толщины покровного слоя d_c позволяло менять положение слоя квантовых точек или квантовых ям в области пространственного заряда почти от границы с поверхностью до границы с квазинейтральной областью структуры. Структуры выращивались методом газофазной эпитаксии из металлорганических (МОС) соединений при атмосферном давлении водорода - газа-носителя паров МОС.

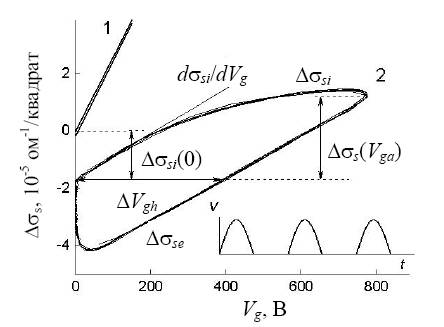
Эффект поля исследовался на разборных МДП структурах металл-диэлектрик-полупроводник (МДП) типа полевых транзисторов с пластинкой слюды толщиной порядка 20 мкм в качестве диэлектрика. Разборная конструкция МДП структуры обеспечивает простоту реализации методики эффекта поля и удобна в том отношении, что ее емкость C_g определяется ем­костью слюдяного конденсатора и практически не зависит от емкости ОПЗ. На управляющий электрод (затвор) подавалось однополупериодное синусоидальное напряжение V_g ( t ) положительной полярности с амплитудой до 800 В (рис. 1), инжектирующее в гетеронаноструктуре основные носители (электроны). К омическим контактам на поверхности гетеронаноструктур (ширина контактов и расстояние между ними = 5 мм) прикладывалось постоянное напряжение V_d около 10 В. Динамическая зависимость квазиповерхностной проводимости ∆ σ_s ( t ) от переменного напряжения на затворе V_g ( t ) после аналого-цифрового преобразования анализировалась на компьютере. При постоянной емкости C_g и отсутствии захвата инжектированных электронов на какие-либо ловушки динамическая зависимость ∆ σ_s ( V_g ( t )) должна быть линейной (рисунок 2.1.1.1, кривая 1), и определенная по ее наклону подвижность в эффекте поля

где dQ_s = C_g dV_g , должна быть равна дрейфовой подвижности электронов в области пространственного заряда μ_n . Захват инжектированных в эффекте поля электронов на поверхностные и объемные ловушки, а также в квантово-размерные состояния приводят к уменьшению наклона динамической зависимости ∆ σ_s ( V_g ( t )) и появлению на ней петли гистерезиса на частотах измерения f ~ (27πτ)^-1 , где τ - время релаксации процесса захвата.