Курсовая работа: Эйлеровы графы
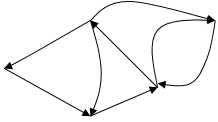
· Ориентированный граф, или орграф, состоит из конечного непустого множества V вершин и заданного набора Х упорядоченных пар различных вершин. Элементы из Х называются ориентированными рёбрами, или дугами. Нет петель и кратных дуг (рис. 3).
 | |||
 | |||
|
| ||
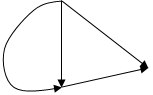
· Направленный граф – это орграф, не имеющий симметричных пар ориентированных рёбер (рис.4).
· Помеченные графы (или перенумерованные), если его вершины отличаются одна от другой какими-либо пометками. В качестве пометок обычно используются буквы или целые числа.[6]
Степенью вершины v i в графе G называется число рёбер, инцидентных v i ,обозначается di . [6] Для орграфа вводятся понятия степени входа и выхода. Степенью выхода вершины v называется количество рёбер, для которых v является начальной вершиной, обозначается outdeg(v ). Степенью входа вершины v называется количество рёбер , для которых v является конечной вершиной, обозначается indeg(v ). Если indeg(v )=0, то вершина v называется источником. Если outdeg(v )=0, то вершина v называется стоком.[1]
Маршруты и связность
Граф G/ (U/ ,V/ ) называется подграфом графа G(U,V), если U/ ÌU и V/ ÌV. Обозначение: G/ ÌG.
Если V/ =V, то G/ называется остовным подграфом G.[3]
Маршрутом в графе G называется чередующаяся последовательность вершин и рёбер v 0 ,x1 ,v 1 ,…v n-1 ,xn ,v n ; эта последовательность начинается и кончается вершиной, и каждое ребро последовательности инцидентно двум вершинам, одна из которых непосредственно предшествует ему, а другая непосредственно следует за ним. Указанный маршрут соединяет вершины v 0 и v n и его можно обозначить v 0 v 1 v 2 …v n (наличие рёбер подразумевается). Эта последовательность иногда называется (v 0 -v n )-маршрутом. Маршрут замкнут, если v 0 =v n , и открыт в противном случае. Маршрут называется цепью, если все его рёбра различны, и простой цепью, если все вершины (а следовательно, и рёбра ) различны. Замкнутая цепь называется циклом. Замкнутый маршрут называется простым циклом, если все его n вершин различны и n³3.
Граф G называется связным, если любая пара его вершин соединена простой цепью.[6]
Задача о кёнигсбергских мостах.
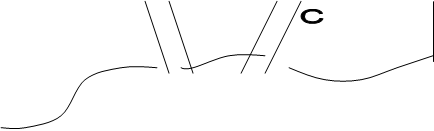
Отцом теории графов является Эйлер (1707-1782), решивший в 1736г. широко известную в то время задачу, называвшуюся проблемой Кёнигсбергских мостов. В городе Кёнигсберге (ныне Калининград) было два острова, соединенных семью мостами с берегами реки Преголя и друг с другом так, как показано на рисунке 5. Задача состояла в следующем: найти маршрут прохождения всех четырёх частей суши, который начинался бы с любой из них, кончался бы на этой же части и ровно один раз проходил по каждому мосту.
 |
 |
![]()
 |  | |||||
 | ||||||
 | ||||||
 | ||||||
Рис.5.
Легко, конечно попытаться решить эту задачу эмпирически, производя перебор всех маршрутов, но все попытки окончатся неудачей. Исключительный вклад Эйлера в решение этой задачи заключается в том, что он доказал невозможность такого маршрута.
Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а каждый мост – линией (ребром), соединяющей соответствующие точки. Получился “граф”. Этот граф показан на рисунке 6, где точки отмечены теми же буквами, что и четыре части суши на рисунке 5.
 |
Рис.6.
Утверждение о не существовании “положительного” решения у этой задачи эквивалентно утверждению о невозможности обойти специальным образом граф, представленный на рисунке 6.
Отправляясь от этого частного случая Эйлер обобщил постановку задачи и нашёл критерий существования обхода у данного графа, а именно граф должен быть связным и каждая его вершина должна быть инцидентна чётному числу рёбер.[6]
Эйлеровы графы
Решение Эйлером задачи о Кёнигсбергских мостах привела к первой опубликованной работе по теории графов. Задачу об обходе мостов можно обобщить и получить следующую задачу теории графов: можно ли найти в данном графе G цикл, содержащий все вершины и все рёбра? Граф, в котором это возможно, называется эйлеровым. Таким образом, эйлеров граф имеет эйлеров цикл – замкнутую цепь, содержащую все вершины и все рёбра. Ясно, что эйлеров граф должен быть связным.[6]
Если снять ограничения на замкнутость цепи, то граф называется полуэйлеровым.
Теорема 1(критерий):
Граф с более чем одной вершиной имеет эйлеров цикл тогда и только тогда, когда он связный и каждая его вершина имеет чётную степень.
Доказательство: Предположим, что граф G имеет эйлеров цикл. Граф является связным, так как каждая вершина принадлежит циклу. Для всякой вершины v графа G каждый раз, когда эйлеров цикл проходит через v , он вносит 2 в степень v . Поэтому степень v чётная.
Обратно, нужно показать, что каждый связный граф, у которого степени вершин чётные, имеет эйлеров цикл. Докажем эту теорему, используя индукцию по числу вершин. Поскольку теорема тривиально справедлива при n£3, начнём индукцию с n=3. Предположим, что каждый связный граф, имеющий менее k вершин, и все вершины которого обладают чётной степенью, содержит эйлеров цикл. Пусть G – связный граф, содержащий k вершин, степени которых чётные. Допустим, что v 1 и v 2 - вершины графа G. Поскольку граф G – связный, существует путь из v 1 в v 2 .Поскольку степень v 2 – чётная, существует неиспользованное ребро, по которому можно продолжить путь. Поскольку граф конечный, то путь, в конце концов, должен вернуться в v 1 , и эйлеров цикл С1 можно считать построенным. Если С1 является эйлеровым циклом для G, тогда доказательство закончено. Если нет, то пусть G/ - подграф графа G, полученный удалением всех рёбер, принадлежащих С1 . Поскольку С1 содержит чётное число рёбер, инцидентных каждой вершине, каждая вершина подграфа G/ имеет чётную степень.
Пусть e – ребро графа G/ , пусть Ge – компонента графа G/ , содержащая е. Поскольку G/ имеет менее, чем k, вершин, и у каждой вершины графа G/ чётная степень, граф G/ имеет эйлеров цикл. Пусть С2 . Далее у С1 и С2 имеется общая вершина, допустим, а. Теперь можно продолжить эйлеров цикл, начиная его в а, пройти С1 , вернуться в а, затем пройти С2 и вернуться в а. Если новый эйлеров цикл не является эйлеровым циклом для G , продолжаем использовать этот процесс, расширяя наш эйлеров цикл, пока, к конце концов, не получим эйлеров цикл для G .[1]
Из теоремы 1 следует, что если в связном графе G нет вершин с нечётными степенями, то в G есть замкнутая цепь, содержащая все вершины и все рёбра графа G. Аналогичный результат справедлив для связных графов, имеющих некоторое число вершин с нечётными степенями.
Следствие 1(а): Пусть G- связный граф, в котором 2n вершин имеют нечётные степени, n>1. Тогда множество рёбер графа G можно разбить на n открытых цепей.
Следствие 1(б): Пусть G- связный граф, в котором две вершины имеют нечётные степени. Тогда в G есть открытая цепь, содержащая все вершины и все рёбра графа G (и начинающаяся в одной из вершин с нечётной степенью, а кончающаяся в другой).[6]
Эйлеровым путём в графе называется путь, содержащий все рёбра графа. Эйлеров путь называется собственным, если он не является эйлеровым циклом.[1]
Теорема 2: Если граф G обладает эйлеровым путём с концами А и В (А не совпадает с В), то граф G связный и А и В – единственные нечётные его вершины.
Доказательство: Связность графа следует из определения эйлерова пути. Если путь начинается в А, а заканчивается в другой вершине, то и А и В – нечётные даже если путь неоднократно проходил через А и В. В любую другую вершину графа путь должен был привести и вывести из неё, то есть все остальные вершины должны быть чётными.