Курсовая работа: Экономико математическая модель

,тыс.руб

затраты на оплату труда тыс.руб. материальные затраты, тыс.руб 2,408806699

амортизация,

тыс.руб.

3,868284073 2,567683844

полная себестоимость,

тыс.руб

7,274210595 4,854902951 4,836609752 tтабличное 2,200985159

Таблица 7

Расчет производился в оболочке «Excel» вручную по формуле (1), t_{табличное} рассчитывалось с помощью функции СТЬЮДРАСПОБР исходя из той же формулы.

Выводы: в результате сравнения t_{расчетное} и t_{табличное} выяснилось, что с вероятностью 0,95 можно утверждать , что связь между результативным и факторными признаками является существенной (t_{расчетное} › t_{табличное} ), неслучайной. Какую из этих двух модель лучше выбрать покажет дальнейший анализ.

4. Регрессионный анализ данных.

На этом этапе, используя метод наименьших квадратов, строится многофакторная регрессионная зависимость(уравнение регрессии) результирующего показателя от оставшейся после предшествующих шагов анализа факторных показателей.

Линейная модель ,содержащая независимые переменные только в первой степени, имеет вид:

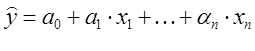(2)

где а₀ – свободный член,

а_1… а_n – параметры уравнения (коэффициенты регрессии),

х_1…. х_n – значения факторных признаков.

Параметры уравнения регрессии рассчитываются методом наименьших квадратов , при этом решается система нормальных уравнений с к+1 неизвестными.

Для измерения степени совокупности влияния отобранных факторов на результативный признак рассчитывают совокупный коэффициент детерминации R² и совокупный коэффициент множественной корреляции R – общие показатели тесноты связи признаков. Пределы изменения : 0 ≤ R ≥ 1. Чем ближе R к 1 , тем точнее уравнение множественной линейной регрессии отражает реальную связь.

Проверка значимости моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. Значимость коэффициента регрессии осуществляется с помощью t – критерия Стьюдента ( отношение коэффициента регрессии к его средней ошибке):

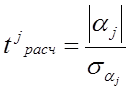(3)

Коэффициент регрессии считается статистически значимым , если t_{расчетное} › t_{табличное} с заданными параметрами (уровнем значимости α, = 0,05, и числом степеней свободы υ = n - к -1, где n – число наблюдений, к – число факторных признаков).

Проверка адекватности модели осуществляется с помощью F – критерия Фишера и величины средней ошибки аппроксимации, которая не должна превышать 12 – 15% . Если величина F_{расчетное} > F_{табличное} , то связь признается существенной. F_{табличное} находиться при заданном уровне значимости α = 0,05 и числе степеней свободы v₁ =k и v₂ = n-k-1. (4)

Модель без учета «Материальных затрат»

В таблице 8 сгенерированы результаты по регрессионной статистике.

Регрессионная статистика
Множественный R	0,997434896
R-квадрат	0,994876372
Нормированный R-квадрат	0,993168496
Стандартная ошибка	2219,306976
Наблюдения	13

Таблица 8

Эти результаты соответствуют следующим статистическим показателям:

Множественный R – коэффициент корреляции R,

R-квадрат – коэффициент детерминации R² ;

F табличное

3,862548358

В таблице 9 сгенерированы результаты дисперсионного анализа, которые используются для проверки значимости коэффициента детерминации R² .

Таблица 9

df	SS	MS	F	Значимость F
Регрессия	3	8607337323	2869112441	582,5226438	1,2734E-10
Остаток	9	44327911,1	4925323,455
Итого	12	8651665234

Df – число степеней свободы, SS – сумма квадратов отклонений,

MS - дисперсия MS, F – расчетное значение F-критерия Фишера,

Значимость F – значение уровня значимости, соответствующее вычисленному F;

Коэффи циенты	Стандарт ная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
полная себесто- имость, тыс.руб	2857,593011	1130,014906	2,528810014	0,094646561	603,5411613	6318,727183
сырье, м погонный	132,3000047	8,941959918	14,79541464	1,27093E-07	112,071886	152,5281233
затраты на оплату труда, « 1 2 3 4 5 6 » К-во Просмотров: 408 Бесплатно скачать Курсовая работа: Экономико математическая модель >>> Скачать <<< Меню Поиск