Курсовая работа: Электромеханические переходные процессы

. (37)

При отключении выключателей, когда разность мощностей внезапно изменяется от до (от до ), приращение угла в n+1 интервале определяется по выражению:

. (42)

По этому алгоритму расчёт продолжается либо до начала уменьшения угла d, что свидетельствует о сохранении устойчивости, либо до предельного по условиям устойчивости угла d_кр .

Результаты расчёта записываем в таблицу 1.

Таблица 1 - Расчёт динамической устойчивости

t, c	d	DP, о.е.	a	Dd
0,00	14.539	0.277	14.516	1.04
0,05	15.579	0.258	13.5	2.973
0,1	18.522	0.203	10.623	4.065
			4.62
0,15	22.617	0.0092	-0.483	3.996
0,2	26.613	-0.102	-5.355	2.462
			-16.059
0,25	29.075	-0.38	-19.887	-.386
0,3	28.689	-0.369	-19.292	-3.15
0,35	25.539	-0.274	-14.363	-5.207
0,4	20.332	-0.113	-5.933	-6.057
0,45	14.275	0.081	4.232	-5.451
0,5	8.824	0.26	13.619	-3.666
			11.309

По результатам данного расчёта строим зависимости d = f(t) и a= f(t) с обозначением характерных углов и соответствующих значений времени.

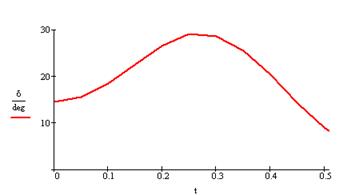
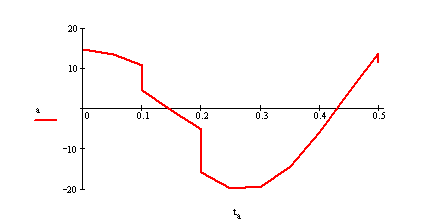
Рисунок 8 – Зависимости угла и ускорения от времени

3.4 Уточнённый расчет динамической устойчивости

При выполнении уточнённого расчёта для конкретности принимается, что изменение синхронной ЭДС E_qe происходит до установившегося значения по экспоненциальному закону с постоянной времени Т_е . Максимальная кратность тока возбуждения и соответствующая ЭДС принимается равной Е_{qe пр.} =5. При этом к дифференциальному уравнению движения ротора добавляется дифференциальное уравнение переходной ЭДС и уравнение изменения синхронной ЭДС:

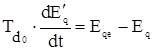; (43)

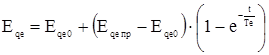, (44)

где T_{d о} – постоянная времени обмотки возбуждения;

Т_е – постоянная времени возбудителя.

В этих выражении (43) синхронная ЭДС Е_q является величиной переменной. Для гидрогенератора при простейшей электропередаче её изменение во времени описывается выражением

.

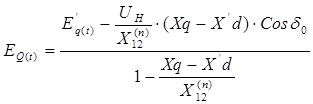(45)

При выполнении уточнённого расчёта с учётом реакции якоря и действия АРВ совместно с уравнением движения ротора решается дифференциальное уравнение (43) с учётом выражения (44). Расчёт выполняется в следующем порядке:

1. Для исходного режима определяются значения начального угла d_о , E'_{q о} , E_{q е} = и среднее значение E_{qe (1)ср} за расчётный интервал времени:

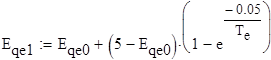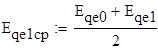Вычисляются взаимные индуктивные сопротивления для всех расчётных ситуаций. При этом гидрогенератор вводится в схему замещения сопротивлением Х_d :

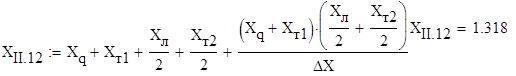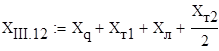(46)

2. По выражению (45) вычисляется ЭДС для первого момента нарушения режима Е_{q (0)} =1,696 о.е..

3. Определяется изменение переходной ЭДС в течении первого расчётного интервала

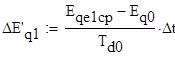(47)

и величина переходной ЭДС в конце первого интервала

(48)

4. Находится активная мощность генератора в начале первого интервала