Курсовая работа: Электропривод с вентильной машиной

В уравнениях (6) значения проекций потока и напряжения на неподвижные оси координат связаны между собой за счёт датчика положения ротора (ДПР, рис. 1). В реверсивных электроприводах ДПР устанавливается таким образом, чтобы пространственный вектор напряжения был сдвинут на 90 электрических градусов относительно пространственного вектора потока. В этом случае проекции пространственных векторов на оси запишутся в виде:

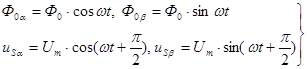(7)

При анализе обычно вводятся относительные переменные. В качестве базовых величин принимаются:

, , ,

где - напряжение на фазе двигателя; - сопротивление фазы двигателя; - число пар полюсов двигателя; - магнитный поток ротора; - скорость вращения холостого хода.

В относительных величинах уравнения (6) с учётом (7) запишутся в виде:

(8)

где относительные переменные и параметры определены выражениями:

, , , , , ,

Модель вентильной машины, составленная по уравнению (8) в пакете MATLAB 6.5, представлена на рис. 4. Базовые значения переменных и относительные параметры машины приведены в таблице 2 приложения.

Рис. 4. Модель вентильной машины в неподвижной системе координат (модель двигателя ДБМ150-4-1,5-2).

Моделирование осуществляем для двигателей ДБМ150-4-1,5-2 и ДБМ185-6-0,2-2. Данные двигателей приведены в таблице 1 приложения. Результаты моделирования представлены на рис. 5 и рис. 6.

Блоком Step задавался скачок относительно входного сигнала равным единице. Исходя из полученных результатов моделирования, можно сделать вывод, что с точки зрения динамического звена ВМ близка по своим характеристикам к машине постоянного тока.

Рис. 5. Переходные процессы в ВМ по моменту и скорости в двигателе ДБМ150-4-1,5-2.

Рис. 6. Переходные процессы в ВМ по моменту и скорости в двигателе ДБМ185-6-0,2-2.

Модель вентильной машины во вращающейся системе координат

При анализе вентильной машины обычно используется вращающаяся со скоростью ротора система координат.

Связь между вращающейся и неподвижной системами координат рассмотрена ниже.

, ,

(9)

, ,

При переходе к вращающимся координатам уравнение электрического равновесия (первое уравнение системы 5) преобразуется к виду:

(10)

Разложив результирующие вектора электромагнитных переменных состояния по осям и , получим скалярное описание машины. При этом ось совмещается с осью потока ротора (см. рис. 2).

(11)

где принято