Курсовая работа: Фигуры постоянной ширины. Треугольник Рело

Несимметричные кривые представляют собой почти произвольные фигуры. Рассмотрим какой-либо набор пересекающихся прямых. Рассмотрим один из секторов. Проведём дугу окружности произвольного радиуса с центром в точке пересечения прямых, определяющих этот сектор. Возьмём соседний сектор, и с центром в точке пересечения прямых, определяющих его, проведём окружность. Радиус подбирается такой, чтобы уже нарисованный кусок кривой непрерывно продолжался. Будем так делать дальше. Оказывается, при таком построении кривая замкнётся и будет иметь постоянную ширину.

Также существуют трёхмерные аналоги кривых постоянной ширины – тела постоянной ширины. Сфера — не единственное тело, которое может вращаться внутри куба, все время касаясь всех шести его граней. Этим же свойством обладают все тела постоянной ширины. Простейшим примером несферического тела постоянной ширины может служить тело, образующееся при вращении треугольника Рело вокруг одной из его осей симметрии. Существует бесконечно много и других тел постоянной ширины. Те из них, которые имеют наименьший объем при данной ширине, получаются из правильного тетраэдра, так же как треугольник Рело — из равностороннего треугольника (рис.7).

Рис.12 Тела постоянной ширины.

4. Треугольник Рело

4.1 Исторические сведения

Рассмотрим подробнее наиболее известную фигуру - треугольник Рело, названный по имени придумавшего его механика Франца Рело – немецкого учёного-инженера, жившего с1829 по 1905 г.г.. В 1852 он окончил политехникум в Карлсруэ, с 1856 профессор Политехнического института в Цюрихе, в 1864—96 профессор Промышленного института (позже — Высшая техническая школа) в Берлине. В 1875 впервые четко сформулировал и изложил основные вопросы структуры и кинематики механизмов, которые ранее содержались в неявной форме в работах П. Л. Чебышева и др.. Рело дал определение кинематической пары, кинематической цепи и механизма как кинематической цепи принуждённого движения; предложил способ преобразования механизмов путём изменения стойки и путём изменения конструкций кинематических пар. Связал теорию механизмов и машин с проблемами конструирования, например, впервые поставил и пытался решить проблему эстетичности технических объектов. Имея в виду это направление его работ, современники Рело называли его поэтом в технике. Творчество Рело оказало значительное влияние на последующие исследования по теории механизмов.

Эта фигура обладает частью важнейших свойств круга. Построить это треугольник просто. Начертим равносторонний треугольник. Заменим его стороны дугами окружностей, центрам которых являются вершины, а радиусами – стороны треугольника (на любом правильном нечётном n-угольнике можно построить кривую постоянной ширины по той же схеме, что и треугольник Рело). На самом деле эта фигура не является треугольником. Треугольник Рело имеет постоянную ширину, равную стороне исходного треугольника. Его также можно использовать в качестве катка при перемещении поверхности, но его гораздо сложнее изготовить, чем круг.

Построим пару параллельных прямых, касающихся треугольника Рело. Проведём ещё пару касательных, перпендикулярных первой паре. Фигура окажется "запертой" в квадрате и будет касаться каждой из его сторон. При вращении фигуры в квадрате она будет постоянно прилегать ко всем сторонам квадрата.

4.2 Очертание четырёхугольника

Наиболее известное свойство треугольника Рело – очертание четырёхугольника сложенным вращением этого треугольник (рис.8).

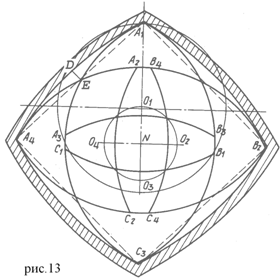
Если вращать треугольник А₁ В₁ С₁ вокруг центра О₁ описанной вокруг него окружности с радиусом О₁ А₁ , а центр треугольника О₁ вращать в противоположную сторону в три раза быстрее по окружности с центром N, то треугольник очертит фигуру, которая незначительно отличается от четырёхугольника. А именно, за один оборот центра О₁ направо по окружности с радиусом О₁ N два угла четырёхугольника будут оформлены вершиной А треугольника Рело и по одному – вершинами В и С, т.е. через каждую четверть оборота вокруг центра N треугольника Рело будет находиться в положении А₂ В₂ С₂ , А₃ В₃ С₃ иА₄ В₄ С₄ .

Выполненные на рисунке построения показывают небольшую кривизну сторон четырёхугольника, о которой также указывают инженеры. По их данным, наибольшее отклонение стороны от идеальной прямой имеет место в середине стороны. Треугольник Рело при вращении контактирует с точкой D серединой своей стороны.

Обозначим через R- радиус, описанного около треугольника Рело круга, r=О₁ N. Тогда

А₁ В₁ =А₂ В₂ =А₃ В₃ =А₄ В₄ =R,

ND=rR+R

Из треугольника А₁ NА₄ получаем

А₁ N=rR, NЕ=

Из равенства DE=ND=NE следует, что

DE= r – R + R,

DE=R(1)+r(1)0,025R+0,293r.

Вычислив кривизну, получаем:

DE ~ 0.025R + 0.293r

Таким образом, отклонение DE стороны квадрата от сделанной прямой зависит, в первую очередь, от радиуса r и не может быть устранено, потому что R и r не могут равняться нулю.

4.3 Движение вершины и центра треугольника Рело

Попробуем построить траектории движения двух характерных точек треугольника Рело при качении его по плоской горизонтальной поверхности. Такими точками будут одна из вершин треугольника и его геометрический центр. Моделирование одного полного оборота треугольника Рело показано на рисунке.

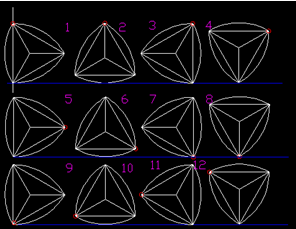
Рис.14

На фигурах 2, 6, 10 треугольник катится по поверхности окружности, на фигурах 4, 8, 12 треугольник переваливается через вершину, на остальных фигурах происходит смена характера движения треугольника с качения на переваливание и наоборот. Рассмотрим движение вершины треугольника. На фигурах 1, 2, 3 помеченная вершина движется линейно, по прямой (Рис. 10). Фактически помеченная вершина является центром вращения окружности, элементом которой является поверхность стороны треугольника Рело. На фигуре 3 помеченная вершина меняет траекторию движения с прямолинейной на траекторию движения по окружности с радиусом, равным длине стороны, по которой он движется на фигурах 3, 4, 5.