Курсовая работа

студента ІV курса

физического факультета

Лукияненко Наталии Петровны

Научный руководитель

Канд. физ.-мат. наук Кошкин Н.И.

О д е с а - 2004

ОГЛАВЛЕНИЕ

Введение

ГЛАВА 1. CEMEЙСТВА АСТЕРОИДОВ И ИХ СВОЙСТВА

1.1. Методы идентификации семейств астероидов

1.2.Физические и динамические свойства членов семейств

ГЛАВА 2. ИССЛЕДОВАНИЕ ЦВЕТОВЫХ ХАРАКТЕРИСТИК АСТЕРОИДОВ ДЛЯ УТОЧНЕНИЯ СОСТАВА СЕМЕЙСТВ

Заключение

Список литературы

Введение

Снующие между планетами невидимые простым глазом астероиды образовали сложную систему в Солнечной системе. Они образовались около 4,5 млрд. лет назад, когда рождалась Солнечная система. Планеты земной группы (Меркурий, Венера, Земля и Марс) выросли в результате объединения подобных тел — планетоземалей. Астероиды движутся, в основном, в так называемом кольце астероидов между орбитами Марса и Юпитера. Пояс астероидов не однородный как может показаться на первый взгляд. Его неоднородность обусловлена сгущениями назваными семействами. Границы семейств проводятся не всегда уверенно, но сам факт наличия семейств среди астероидов несомненен. По разным критериям к членам семейств относят от 45 до 75% всех астероидов, а число семейств, видимо, превышает 200. А поскольку группы астероидов на сходных орбитах могут быть осколками разрушенного более крупного тела, которое, возможно, состояло из однородного вещества, то семейство должно иметь повышенную минералогическую однородность. А общая картина всего главного пояса астероида состоящего из множества семейств предполагает быть таксономически неоднородной.

В данной работе используется несколько каталогов, а в частности: (SloanDigitalSkySurveyMovingObjectCatalog (2001 г.), AsteroidDynamicalFamilies (1995г.)). В нем представлена широкополосная u, g, r, i, и z (_eff = 0.3551, 0.4686, 0.6166, 0.748 и 0.8932 m) фотометрия. Каталог содержит около 50000 подвижных объектов, из которых в настоящее время отождествлено около 12000 астероидов и приводит так же их оскулирующие и собственные элементы. В каталоге Asteroid Dynamical Families (1995г.) представлены 12487 астероидов с вычисленными собственными элементами. Из них около 5000 астероидов отнесены к 63 семействам. Этот каталог семейств использовался нами для определения границ семейств в собственных элементах a’, e’, sin(i’).

Глава I .

Семейства астероидов и их свойства

1.1. Методы идентификации семейств астероидов

Название “астероидные семейства” исторически связано с именем японского астронома Хиротсума Хираямы [1], который первым ввёл понятие “собственных” орбитальных элементов, чтобы идентифицировать группировки астероидов, которые характеризуются почти близкими собственными элементами.

Усредненные результаты численного интегрирования элементов орбиты астероида можно представить как сумму “свободных колебаний” и “вынужденной” компоненты, обусловленной планетными возмущениями. На рис.1 показано сглаженное изменение эксцентриситета орбиты астероида e за 20000 лет, которое равно векторной сумме “вынужденного” эксцентриситета f и постоянного “собственного” эксцентриситета e_p . Аналогично в осях q=sin(i )cos(Ω), p=sin(i )cos(Ω) определяется “собственное” наклонение орбиты sin(i_p ). А “усредненное” по времени значение большой полуоси принимается за “собственную” полуось a_p .

Хираяма сделал гипотезу, что близость собственных элементов целого ряда астероидов не может быть случайностью, что члены семейства являются фрагментами, которые появились в результате разрыва общего родительского тела. В своём классическом анализе, Хираяма отожествил пять семейств. Они и сегодня известны, как семейства Хираямы: Эос, Фемида, Коронис, Флора и Мария. Прошло несколько лет, прежде чем проблема идентификации астероидных семейств была снова затронута. К небольшому списку Хираямы начали добавлять много новых астероидных семейств. Благодаря развитию более объективных математических методов идентификации, начиная с 1990 года ситуация в области идентификации семейств значительно улучшилась. Кроме того, появляется всё больше и больше наборов точных собственных элементов, что позволяет исследователям анализировать всё более обширные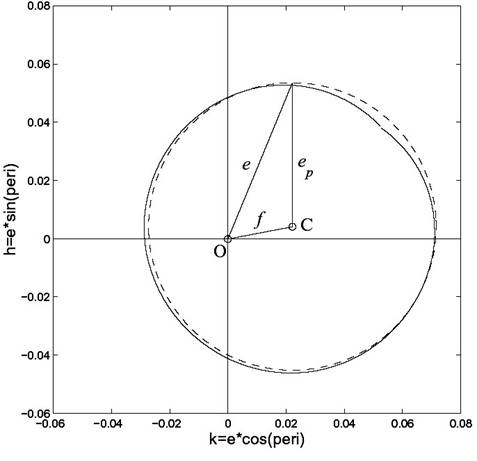
списки астероидных орбит.

Рис. 1.

Собственные элементы очень важны для идентификации семейств, но они могут изменятся, как следствие планетарных возмущений. Оскулирующие орбиты семейства сформировались после раскола родительского тела, близки только сразу после формирования семейства, но потом начинают быстро отклоняться, вследствие эффекта возмущений. Для целей идентификации семейств, важный факт – то, что оскулирующие элементы членов семейств изменяются как функция времени, но собственные элементы не являются функцией от времени, поэтому, возможно анализировать похожие орбиты объектов, исследуя их собственные элементы, а не оскулирующие. В частности усовершенствование динамических теорий и вычислительных методов привело к тому, что появилось много данных о собственных элементах астероидов. Но с другой стороны, применяя различные идентифицирующие методы к набору данных собственных элементов, мы видим несоответствия в списках семейств, полученных различными авторами. Рассмотрим подробнее два наиболее употребимых идентифицирующих метода.

Метод иерархической кластеризации . Метод основан на классической процедуре построения иерархического дерева для целей классификации. Zappalaи др [2],[3]. приспособили и оптимизировали этот метод для идентификации существующих группировок в трёхмерном пространстве собственных элементов. Для этого вводится метрика расстояний

d = n *a * sqrt {C_a * (a /a )² + C_e * (e )² + C_i * (sini )² },

где n – среднее суточное движение астероида, a – большая полуось его орбиты, C_a , C_e , C_i – постоянные параметры (обычно используются значения C_a =5/4, C_e =2 и C_i =2). Чтобы получить дерево, на каждом шаге процедуры объединяют два самых близких объекта рассмотренной выборки в единый объект и затем повторяют этот процесс до того, пока остаётся один единственный объект. На каждом шаге расстояние d(i,j,k) между объединяемыми объектами i и j и общим объектом k определяется как минимум из двух d(i,k) и d(j,k). В результате получают так называемые «сталактитовые диаграммы». Сравнивая сталактиты, полученные от реального набора данных и полученные от модельных квазислучайных совокупностей точек в фазовом пространстве собственных элементов, возможно указать кластеры [9], которые являются статически существенными (значимыми), т.е. моделирование позволяет провести границу, ниже которой все обнаруженные группировки можно считать реальными семействами.

Метод вайвлет–анализа . Это метод оценки плотности точек, основанный на использовании специфической функции, названной «вайвлетом» [2]. Использование этого метода позволяет обнаружить местные уплотнения точек, принадлежащих N-мерному пространству в различных масштабах. При наложении некоторой сетки в фазовом пространстве, возможно вычислить коэффициенты вайвлета в каждом её узле. Чем больше значение этого коэффициента, тем более плотная группировка обнаруживается около этого узла и, наоборот, чем ближе к нулю этот коэффициент, тем более однородно локальное распределение. Используя эту методику для квазислучайных распределений точек можно оценить уровень обнаруживаемости реальных группировок. Оба эти метода часто применяются в последние годы. Они выделяют, как правило, одни и те же семейства, хотя к членам семейства они относят разное количество астероидов.

1.2. Физические и динамические свойства членов семейств

Распределение астероидов по размерам. Важной физической характеристикой семейств, связанной с их эволюцией, служит распределение членов семейства по массам и размерам [4]. Масса астероида, как правило, определяется по значению абсолютной звездной величины, которую можно вычислить по измеренному значению видимой звездной величины в точке орбиты малой планеты с известными координатами. Постоянными, входящими в это соотношение, являются: альбедо поверхности астероида p и плотность его вещества . Принимая значение p=0.24 и =3 г/см³ :

LgM=25.834-0.6g,

где масса М выражена в граммах.

Восстановление поля скоростей осколков, образовавшихся при образовании семейства . Структура семейств в пространстве собственных элементов используется, чтобы получить информацию относительно скоростей выброса фрагментов в формирующих семейства событиях. Мы можем интерпретировать различия в орбитальных элементах в терминах различий в скорости выброса из первоначального родительского тела. Преобразования скоростей в орбитальные элементы или наоборот даются Гауссовыми формулами, которые могут быть записаны следующим образом, согласно предположению, применимому для семейств, что скорости выброса являются намного меньшими, чем орбитальная скорость родительского тела.

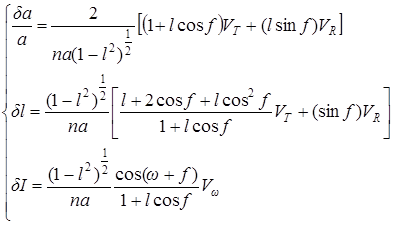
где na – средняя орбитальная скорость. V_T , V_R , V_w - являются компонентами вектора скорости выброса по направлению движения, по радиусу орбиты и нормали к орбитальной плоскости. Параметры f и w – истинная аномалия и аргумент перигелия в момент его разрушения. Эти углы заранее неизвестны, и этот факт долго мешал попыткам восстановления начальных полей скорости выброса по наблюдаемым местоположениям членов семейств в пространстве собственных элементов.

С помощью многочисленных числовых моделей Zappalaи др. (1996) [5] была показана возможность построения поля скоростей, особенно когда они не случайны, а могут быть сферическими, эллипсоидальными, коническими и более сложной формы. Основная идея состоит в том, чтобы использовать некоторые безразмерные параметры для оценки наиболее вероятных значений неизвестных углов f и w . Сделать такую модель можно только тогда, когда у нас есть достаточное количество членов. Во многих ситуациях структура поля была найдена, например в случае Весты, Доры, Мерксии и Марии. Восстановленные поля оказываются вообще симметричными и подобными тем, что были получены в лабораторных экспериментах по высокоскоростным соударениям. Следует иметь в виду, что семейства идентифицируются в собственных орбитальных элементах, а формулы Гаусса описывают поведение в пространстве оскулирующих элементов. Однако, согласно Бенджоя и др. (1993) [5] полная структура поля скоростей выброса сохраняется в преобразовании от оскулирующих к собственным элементам. Главный эффект преобразования будет состоять в параллельном переносе всех векторов скорости при сохранении структуры поля.

С одной стороны на длинном временном промежутке постоянство собственных элементов не сохраняется, что делает нахождение поля скоростей сложным. С другой стороны, возможно, что на длинных временных промежутках семейства могут вообще исчезать из-за прогрессивной столкновительной эрозии [11].

--> ЧИТАТЬ ПОЛНОСТЬЮ <--