Курсовая работа: Физические величины и их измерения
Анализ величин позволяет разделить (рис. 1) их на два вида: величины материального вида (реальные) и величины идеальных моделей реальности (идеальные), которые относятся главным образом к математике и являются обобщением (моделью) конкретных реальных понятий.
Реальные величины, в свою очередь, делятся на физические и нефизические. Физическая величина в самом общем случае может быть определена как величина, свойственная материальным объектам (процессам, явлениям), изучаемым в естественных (физика, химия) и технических науках. К нефизическим величинам следует отнести величины, присущие общественным (нефизическим) наукам – философии, социологии, экономике и т.п.
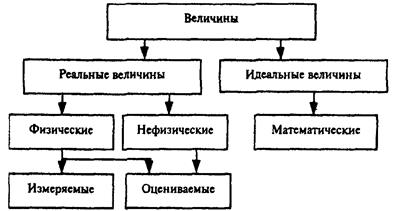
Рис. 1. Классификация величин.
Документ РМГ 29-99 трактует физическую величину как одно из свойств физического объекта, общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них. Индивидуальность в количественном отношении понимают в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого.
Физические величины целесообразно разделить на измеряемые и оцениваемые. Измеряемые ФВ могут быть выражены количественно в виде определенного числа установленных единиц измерения. Возможность введения и использования таких единиц является важным отличительным признаком измеряемых ФВ. Физические величины, для которых по тем или иным причинам не может быть введена единица измерения, могут быть только оценены. Под оцениванием понимается операция приписывания данной величине определенного числа, проводимая по установленным правилам. Оценивание величины осуществляется при помощи шкал. Шкала величины — упорядоченная совокупность значений величины, служащая исходной основой для измерения данной величины.
Нефизические величины, для которых единица измерения в принципе не может быть введена, могут быть только оценены. Следует отметить, что оценивание нефизических величин не входит в задачи теоретической метрологии.
Для более детального изучения ФВ необходимо классифицировать, выявить общие метрологические особенности их отдельных групп. Возможные классификации ФВ приведены на рис. 2.
По видам явлений ФВ делятся на:
• вещественные, т.е. величины, описывающие физические и физико-химические свойства веществ, материалов и изделий из них. К этой группе относятся масса, плотность, электрическое сопротивление, емкость, индуктивность и др. Иногда эти ФВ называют пассивными. Для их измерения необходимо использовать вспомогательный источник энергии, с помощью которого формируется сигнал измерительной информации. При этом пассивные ФВ преобразуются в активные, которые и измеряются;
• энергетические, т.е. величины, описывающие энергетические характеристики процессов преобразования, передачи и использования энергии. К ним относятся ток, напряжение, мощность, энергия. Эти величины называют активными.
Они могут быть преобразованы в сигналы измерительной информации без использования вспомогательных источников энергии;
• характеризующие протекание процессов во времени, К этой группе относятся различного вида спектральные характеристики, корреляционные функции и другие параметры.
По принадлежности к различным группам физических процессов ФВ делятся на пространственно-временные, механические, электрические и магнитные, тепловые, акустические, световые, физико-химические, ионизирующих излучений, атомной и ядерной физики.
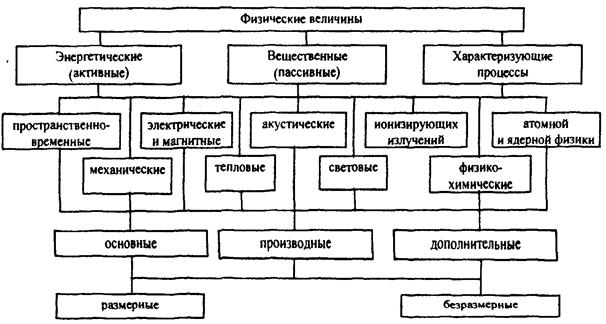
Рис. 2. Классификации физических величин
По степени условной независимости от других величин данной группы все ФВ делятся на основные (условно независимые), производные (условно зависимые) и дополнительные. В настоящее время в системе СИ используются семь физических величин, выбранных в качестве основных: длина, время, масса, температура, сила электрического тока, сила света и количество вещества. К дополнительным ФВ относятся плоский и телесный углы. По наличию размерности ФВ делятся на размерные, т.е. имеющие размерность, и безразмерные.
1.2 Метрическая система мер
Отсутствие рациональных обоснований при выборе единиц ФВ привело к их большому разнообразию не только в разных странах, но даже в разных местностях одной страны. Это создавало большие трудности, особенно в международных отношениях. Возникла метрическая система мер, т.е. совокупность единиц ФВ, рекомендованных вместо применявшихся ранее.
Были приняты единицы: длины – метр (м), массы – килограмм (кг), объема – литр (л), времени - секунда (с).
Были также введены десятичные кратные и дольные единицы ФВ, т. е. единицы ФВ, в 10 в целой степени раз большие и меньшие, и установлены простые правила присвоения наименований кратным и дольным единицам ФВ применением приставок: кило, гекто, дека, деци, санти и милли [например, сантиметр (см), миллиметр (мм), декалитр (дал) и т. п.]
Это давало единицам метрической системы (метрическим единицам ФВ) существенное преимущество перед существовавшими в то время другими. Кроме того, метрические единицы ФВ позволяли не применять составные именованные числа (например, длина 8 саженей 3 фута 5 дюймов) и значительно облегчали расчеты.
1.3 Системы единиц физических величин
Построение единиц и систем единиц. Раньше единицы различных ФВ устанавливались, как правило, независимо друг от друга. Исключениями были лишь единицы длины, площади и объема. Основной особенностью современных единиц ФВ является то, что между ними устанавливают зависимости. При этом произвольно выбирают несколько основных единиц ФВ, а все остальные — производные единицы ФВ получают при помощи зависимостей (законов и определений), связывающих различные ФВ, т.е. определяющих уравнений.
Физические величины, единицы которых приняты в качестве основных, называются основными ФВ, а единицы которых являются производными, называются производными ФВ.
Совокупность основных и производных единиц ФВ, охватывающая все или некоторые области физики, называется системой единиц ФВ.
Рассмотрим примеры установления производных единиц ФВ при выбранных в качестве основных ФВ длины L, массы М и времени Т, т.е. при выбранных основных единицах ФВ [L], [М] и [Т].
Пример 1. Установление единицы площади. Выберем какую-либо простую геометрическую фигуру, например круг. Размер площади s круга пропорционален второй степени размера его диаметра d: s = kS d2 , где kS — коэффициент пропорциональности. Это уравнение и возьмем в качестве определяющего. Положив размер диаметра круга равным единице длины, т. е. d = [L], получим [s] = kS [L]2 . Выбор коэффициента пропорциональности kS произволен Пусть kS = l, тогда [s] = [L]2 , т. е. за единицу площади выбрана площадь круга, диаметр которого равен единице длины. Если [L] = 1 м, то [s] = 1 м2 . Площадь круга в этом случае нужно вычислять по формуле s = d2 , а площадь квадрата со стороной b — по формуле s = (4/p)b2 .
Обычно вместо такой круглой единицы площади применяют более удобную квадратную единицу, представляющую собой площадь квадрата со стороной, равной единице длины.