Курсовая работа: Гамильтоновы графы и сложность отыскания гамильтоновых циклов

Федеральное агентство по образованию РФ

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра геометрии

Гамильтоновы графы и сложность отыскания гамильтоновых циклов

КУРСОВАЯ РАБОТА

Научный руководитель

Старший преподаватель ______________

должн., уч. степень, уч. зван. подпись, дата инициалы, фамилия

Саратов 2010

Содержание

Введение

1. Гамильтоновы графы

1.1 Основные определения и результаты

1.2 Теоремы достаточности гамильтонова графа

2. Методы отыскания гамильтоновых циклов

2.1 Алгебраические методы

2.2 Метод перебора Робертса и Флореса

2.2.1 Улучшение метода Робертса и Флореса

Приложение

Заключение

Список литературы

Введение

????? ???? ???????? ?????? ????????: 1. ???????????? ? ????????? ?????????, ?????????? ? ?????????????? ??????? ? ???????.2. ??????????? ?????? ? ?????? ????????? ????????????? ?????? ? ??????3. ???????? ????????? ??? ?????????? ????????????? ??????.?????? ?????, ????? ?????? ??????? ? ???????? ????????????, ???????? ?? ???? ??????????? ????????? ????????? ????? ?????, ??? ???????, ????, ????.????????? ? ????? G (V,E ) ?????????? ???????????? ?????????????????? ?????? ? ?????: ,, ? , , ? ??????? ????? ??? ???????? ???????? ??????????. ???? = , ?? ??????? ???????, ????? ??????.???? ??? ????? ????????, ?? ??????? ?????????? ?????. ???? ??? ??????? (? ??????, ?????) ????????, ?? ??????? ?????????? ??????? ?????.????????? ???? ?????????? ??????; ????????? ??????? ???? ?????????? ??????? ??????. ???? ??? ?????? ?????????? ????????????. ??? ???????? ???? ?????????? ?????, ? ???? ? ????????.

1. Гамильтоновы графы

1.1 Основные определения и результаты

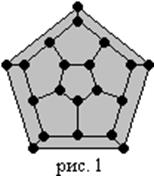
Название «гамильтонов цикл» произошло от задачи «Кругосветное путешествие» предложенной ирландским математиком Вильямом Гамильтоном в 1859 году. Нужно было, выйдя из исходной вершины графа, обойти все его вершины и вернуться в исходную точку. Граф представлял собой укладку додекаэдра, каждой из 20 вершин графа было приписано название крупного города мира.

Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл называется гамильтоновым циклом , а граф называется гамильтоновым графом . Граф, который содержит простой путь, проходящий через каждую его вершину, называется полугамильтоновым. Это определение можно распространить на ориентированные графы, если путь считать ориентированным.

Гамильтонов цикл не обязательно содержит все ребра графа. Ясно, что гамильтоновым может быть только связный граф и, что всякий гамильтонов граф является полугамильтоновым. Заметим, что гамильтонов цикл существует далеко не в каждом графе.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--