Курсовая работа: Гамильтоновы графы и сложность отыскания гамильтоновых циклов

В случае 2) возможны следующие случаи:

a) В графе G существует дуга (xr , x 1 ), и поэтому найден гамильтонов цикл.

b) Дуга (xr , x 1 ) не существует и не может быть получен никакой гамильтонов цикл.

В случаях (1) и (2b) следует прибегнуть к возвращению , в то время как в случае (2a) можно прекратить поиск и напечатать результат (если требуется найти только один гамильтонов цикл), или (если нужны все такие циклы) произвести печать и прибегнуть к возвращению.

Возвращение состоит в удалении последней включенной вершины xr из S , после чего остается множество S = {x 1, a , b , c , … , xr -1 }, и добавлении к S первой возможной вершины, следующей за xr , в столбце xr -1 матрицы M . Если не существует никакой возможной вершины, делается следующий шаг возвращения и т.д.

Поиск заканчивается в том случае, когда множество S состоит только из вершины x 1 и не существует никакой возможной вершины, которую можно добавить к S , так что шаг возвращения делает множество S пустым. Гамильтоновы циклы, найденные к этому моменту, являются тогда всеми гамильтоновыми циклами, существующими в графе.

Рассмотрим пример поиска гамильтонова цикла в графе переборным методом Робертса и Флореса.

Пример:

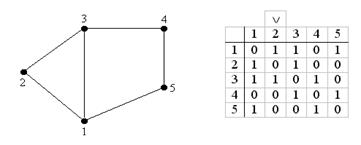
"2"

1) S = {1}

2) S = {1, 2}

3) S = {1, 2, 3}

4) S = {1, 2, 3, 4}

5) S = {1, 2, 3, 4, 5} - Г 4→3 4→5

6) S = {1, 2, 3, 4}

7) S = {1, 2, 3} 3→1 3→2 3→4

8) S = {1, 2}

9) S = {1}

"3"

10) S = {1, 3} 3→2

11) S = {1, 3, 2} 2→1

12) S = {1, 3} 2→3

13) S = {1, 3, 4} 3→4 4→5

14) S = {1, 3, 4, 5, 4} 5→нет

15) S = {1, 3, 4}

16) S = {1, 3}

17) S = {1}

"5"