Курсовая работа: Генератор импульсных напряжений

(1.1)

При выполнении этого условия влиянием индуктивности можно пренебречь и схема замещения упрощается и принимает вид, показанный на рис. 1.5б.

Удовлетворительные результаты расчета могут быть получены при использовании более простых схем замещения (рис. 1.4), полученных из полной схемы замещения при условиях: R_Ф =0 (рис. 1.5 а) и R₁ =0 (рис. 1.5 б).

Рис. 1.6. Схемы замещения разрядной цепи

Эти схемы отличаются друг от друга коэффициентом использования разрядной схемы ГИН. Для дальнейших расчетов принимаем схему, показанную на (рис. 1.6,а).

Для схем рис. 1.6б и рис. 1.6а измерение напряжения на выходе (U₂ ) дается дифференциальным уравнением второго порядка.

(1.2)

Н и l - коэффициенты, зависящие от параметров схемы. Решение этого уравнения относительно U₂ имеет вид:

(1.3)

Р₁ и Р₂ –корни характеристического уравнения; А–постоянная интегрирования, которая может быть определена из граничных условий при t =0

Для схемы рис. 1.6а они запишутся так:

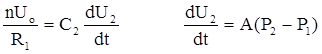(1.4)

n – число ступеней ГИН, U_о – зарядное напряжение ступени.

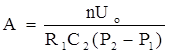(1.5)

Таким образом, напряжение на выходе ГИН описывается выражением [9,10]

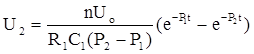(1.6)

1.3 Связь параметров импульса напряжения с параметрами разрядного контура ГИН

Согласно определению длительности стандартного импульса можно записать уравнение (4) в виде:

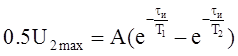(1.7)

t_и – длительность импульса, T₁ и T₂ - постоянные времени. (P₁ = 1/T₁ и P₂ = 1/T₂ ). Так как для стандартных импульсов T₁ >> T₂ , то можно в первом приближении допустить, что вторая экспонента практически равна нулю, и выражение (1.8) имеет вид:

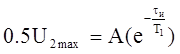(1.8)

Если пренебречь затуханием первой экспоненты в течение длительности фронта импульса, что справедливо для стандартных импульсов, то значение постоянной интегрирования А, с некоторым допущением, можно принять равным амплитудному значению А = U_2max . Тогда решая уравнение (1.7) относительно t_и , получим выражение, которое связывает длительность импульса с параметрами разрядного контура ГИН:

t_и ~ 0.69 T₁ T₁ ~ (R₁ + R2)·(C₁ + C₂ ) (1.9)

Согласно определению длительности фронта импульса для стандартной волны можно записать соотношения:

(1.10)

(1.11)

t₁ и t₂ - значения времени, когда напряжение импульса достигает соответственно 0.3 и 0.9 от амплитудного значения.

Пренебрегая затуханием первой экспоненты в пределах длительности фронта импульса и полагая первую экспоненту равной единице, что справедливо при T₁ >> T₂ , получим

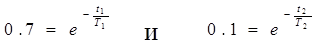Так как (t₂ -t₁ )~0.6, то длительность фронта определяется как:

t_ф = 3.25 T₂ , 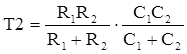(1.12)