Курсовая работа: Генератор импульсных напряжений

Uз = 40 кВ – зарядное напряжение ГИН,

N – число ступеней ГИН.

Определяем минимальное число ступеней ГИН:

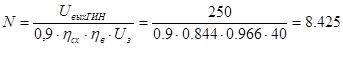. (2.7)

т.к. число ступеней не может быть дробным, округляем его до ближайшего целого значения, т.е. принимаем N=7, почему именно 7, дело в том, что максимальное значение энергии, возможно, получить только в случае того, когда С_гин = С_дфл , С_дфл – емкость двойной формирующей линии, которая в данном случае является нагрузкой. Если имеется 8 ступеней согласовка С_гин = С_дфл отсутствует, поэтому при расчетах убирают 1 ступень и разрабатываю ГИН, который содержит 7 ступеней.

Тогда необходимая емкость конденсатора

С_к =С₁ ·N=6,7·10^-9 ·7=0.047мкФ

Выбираем конденсатор типа К75-74, с емкостью С_К = 0,047мкФ [11,12].

Почему именно такие конденсаторы? Во-первых, очень компактные и габариты конденсатора удобные (длина 24 см, ширина 6см). Во-вторых, индуктивность конденсаторов очень низкая около 100нГн. В-третьих, токи утечки небольшие вследствие минимального сопротивления и, в-четвертых, способны накапливать высокую удельную энергии и пропускать достаточно большие токи.

Конструкция конденсатора: в цилиндрических корпусах из полимерных материалов с разнонаправленными выводами. На рис.2.1. представлен чертеж конденсатора К75-74 с основными параметрами:

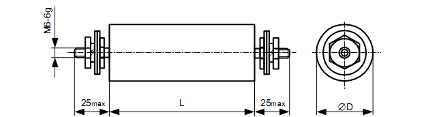
Рис.2.1. Конструктивный вид конденсатора К75-74

Определим, входит ли отношение в интервал:, т.е..

0.062 < 0.08 < 0.160 видим, что отношение входит в интервал, поэтому принимаем число ступеней ГИН N=7 и разрядную емкость ГИН С₁ = 6.7·10^–9 Ф.

По формуле (2.1) рассчитаем коэффициент схемы:

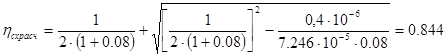
> 0.95·, т.е. 0.844 > 0.762 - условие выполняется

По формуле (2.6) рассчитаем напряжение выдаваемое ГИН:

U_выхГИН = 0,9·N·h_в ·h_сх ^max ·U_З = 0.9 ·9·0.966·0.829· 40 = 230 кВ.

то есть то, что заданно (U_зарГИН =250 кВ) хорошо совпадает с тем, что было рассчитано.

Преобразовав уравнения (1.13) и (1.15) получаем выражения для определения фронтового и разрядного сопротивлений соответственно:

(2.8)

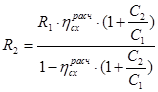(2.9)

Определим фронтовое и разрядное сопротивления:

,

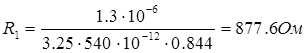
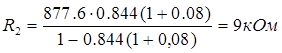где 0.08 = С₂ /С₁ полученное с помощью программы MathCAD.

2.4 Расчет разрядного контура на апериодичность

Для проверки разрядного контура на апериодичность необходимо оценить индуктивность разрядного контура генератора (L_г ), которая должна быть меньше или равна эквивалентной индуктивности(L_э ). Эквивалентная индуктивность определяется из условия отсутствия колебаний в разрядном контуре, которое имеет вид:

R₁ ³R_кр =2, где С_э =С_1· С₂ /(С₁ +С₂ ) (2.10)

При испытании изоляции, в соответствии с требованием ГОСТ, допускаются колебания с амплитудой не более 5% от амплитуды импульса напряжения. С учетом этого условия (2.24) можно записать как:

R₁ ³ 0.69·R_кр =1.38· (2.11)