Курсовая работа: Графы и их представление на ЭВМ
Элементами матрицы смежности являются 0 и 1, Если вершины соединены, то ставится 1 и наоборот.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 |
| 3 | 1 | 0 | 0 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 |
Матрица смежности графа GРис.
2.2.1 Граф и его матрица смежности
Матрица смежности симметрична относительно главной диагонали (рис. 2.2.1).
2. Матрица инцидентности вершин и рёбер содержит m– строк и n– столбцов, где m– количество вершин, n– количество рёбер.
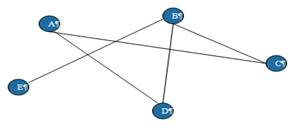
Рис.1
| a | b | c | d | e | |
| A | 0 | 1 | 1 | 0 | 0 |
| B | 1 | 0 | 0 | 1 | 1 |
| C | 0 | 0 | 1 | 0 | 1 |
| D | 0 | 1 | 0 | 1 | 0 |
| E | 1 | 0 | 0 | 0 | 0 |
| F | 0 | 0 | 0 | 0 | 0 |
Рис 2.2.2 Граф и его матрица инцидентности
В любом столбце матрицы инцидентности (рис. 2.2.2) лиши две единички.
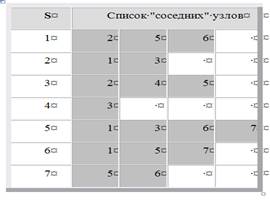
Другой способ представления графа обеспечивает функция, которая выдает списки узлов, с которыми данный узел связан непосредственно. Для графа, отображенного на рис. 2.2.3, такое описание можно представить в виде структуры (таблица 2.1). В колонке s представлены номера узлов, далее в строке таблицы следует список соседних узлов. По этой причине число колонок в каждой из строк различно.
Таблица 2.1
2.3 Представление ориентированных граф
Представление ориентированных граф элементами матриц смежности и инцидентности являются 0, 1, -1. Пусть даны два ориентированных графа (рис. 2.3.1), тогда матрицы смежности и инцидентности для них будут выглядеть как в таблицe2.3

Рис. 2.3.1 Ориентированные графы
Таблица 2.3
| Матрица смежности | |||||||||||||||||||||||||||||||
| A | B | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| Матрица инцидентности | |||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
В матрице инцидентности для ориентированных граф ставится 0 – если вершина и ребро не инцидентны, -1 – если вершина является началом, 1 – если вершина является концом.
3. Виды графов и операции над ними
3.1 Элементы графов
Для рассмотрения видов граф и операций над ними необходимо познакомиться с такими понятиями как подграфы, маршрут, цепь, цикл.
Граф G '( V ', Е') называется подграфом графа G ( V , Е) (обозначается G ' ÌG ), если V ' ÌV и/или Е' ÌЕ.
Если V ' = V , то G ' называется остовным подграфом G .
Если V ' ÌV & Е' ÌЕ & ( V ' ¹ V ÚЕ' ¹ Е), то граф G ' называется собственным подграфом графа G .
Подграф G '( V ' , Е') называется правильным подграфом графа G ( V ,Е), если G ' содержит все возможные ребра G :
" и, v ÎV ' (и, v ) ÎЕ Þ (и, v ) ÎЕ'.
Правильный подграф G '( V ' , Е') графа G ( V , Е) определяется подмножеством вер шин V '.
Маршрутом в графе называется чередующаяся последовательность вершин и ребер в которой любые два соседних элемента инцидентны.
v0 , e1 , v1 , e2 , v2 ,…,ek , vk ,